A figura representa um círculo de centro C com duas cordas paralelas, e
, cujas medidas são PQ = 8 cm e RS = 6 cm. A distância entre C e a corda
é igual a d cm.
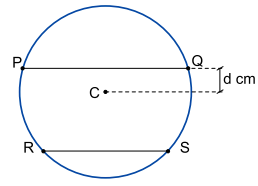
a) Calcule a área do círculo para o caso em que d = 3 cm.
b) Calcule a medida do raio da circunferência para o caso em que a distância entre e
seja de 4 cm.
a) Considere a figura a seguir:
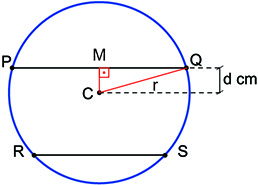
Sejam:
r: o raio da circunferência;
M: o ponto médio do seguimento PQ;
d: a medida do seguimento CM.
No triângulo retângulo CQM, tem-se:
Como, cm e d = 3 cm, tem-se:
Logo a área do círculo é: π∙52 = 25π cm²
Resp.: 25π cm²
b) Considere a figura a seguir:
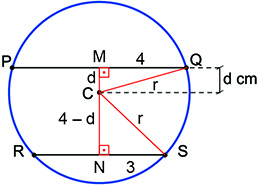
Sejam:
r: o raio da circunferência;
M: o ponto médio do seguimento PQ;
N: o ponto médio do seguimento RS;
d: a medida do seguimento CM.
No triângulo CQM, tem-se:
No triângulo CSN, tem-se:
De ( I ) em ( II ):
Substituindo em ( I ):
Resp.: