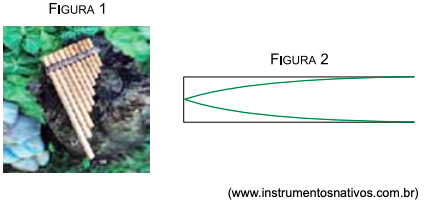
A figura 1 mostra um instrumento musical constituído por vários tubos, abertos em uma extremidade e fechados na outra, colocados lado a lado, e a figura 2 mostra a forma da onda sonora estacionária que corresponde à frequência fundamental de vibração desses tubos.
a) Considerando que a velocidade de propagação das ondas sonoras no ar seja 340 m/s e que a frequência fundamental da onda emitida por um dos tubos desse instrumento seja 170 Hz, calcule, em metros, o comprimento de onda dessa onda e o comprimento desse tubo.
b) A intensidade sonora (I) exprime a quantidade média de energia transportada por uma onda sonora (ΔE) através de uma unidade de área (ΔS) perpendicular à direção de propagação da onda, por unidade de tempo O nível sonoro (β) indica a intensidade do som percebido pelo sistema auditivo humano e é definido, quando medido em dB, como β = 10 log I/I0, sendo I0 = 10–12 W/m2.
Supondo que a superfície da membrana timpânica de uma pessoa seja perpendicular à direção de propagação das ondas sonoras e tenha área de 6,0 × 10–5 m2, calcule a quantidade de energia, em joules, que atinge essa membrana, em um segundo, quando essa pessoa ouve um som de nível sonoro igual a 60 dB.
a) Por meio da expressão , podemos obter o comprimento de onda do som emitido pelo tubo.
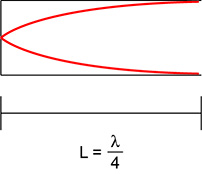
No modo fundamental, o comprimento L do tubo corresponde a vezes o comprimento de onda, conforme indica o esquema:
b) Utilizando a expressão dada do nível sonoro , temos:
Aplicando a definição de logaritmo:
De acordo com a expressão fornecida no enunciado, a quantidade de energia, em joules, que atinge o tímpano, por segundo é:
Em que ΔS é a área da membrana timpânica e vale .
Na equação acima: