O último relatório do Painel Intergovernamental sobre Mudanças Climáticas da ONU (IPCC) mostra que uma parcela significativa do aumento dos níveis dos oceanos vem da expansão térmica da água. Essa expansão ocorre principalmente nas camadas superiores dos oceanos, até cerca de 700 m de profundidade.
O gráfico a seguir mostra a variação da razão v(T) / v(T=6 °C) onde v(T) é o volume de 1 g de água (em cm3 ) à pressão ambiente (também chamado de volume específico) em função da temperatura T expressa em graus Celsius.
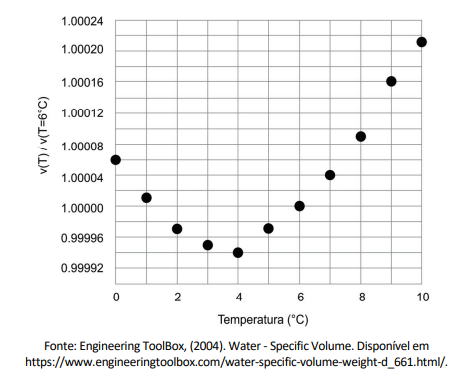
a) Se uma coluna de água inicialmente a uma temperatura de 1 °C for aquecida até 3 °C, sua altura aumenta ou diminui? Justifique com base nos dados do gráfico.
b) Considere uma coluna de água cuja altura a 6 °C é de 700 m. Assumindo que toda a expansão volumétrica ocorra na direção vertical e que sua massa não varie, estime, com base nos dados do gráfico, a variação de altura da coluna quando esta é aquecida de 6 °C até 9 °C. Expresse seu resultado em centímetros.
c) Considere uma coluna de água de 700 m de altura que sofre um aumento de temperatura de 2 °C. Assumindo que a massa dessa coluna de água não varie, desprezando a variação da massa específica da água com a temperatura e admitindo que esta seja constante e igual a 1 g/cm3, calcule o calor absorvido pela coluna por unidade de área de superfície. Expresse seu resultado em J/m2.
Note e adote:
Considere que o volume específico da água (definida pelo inverso da massa específica) não varie com a profundidade.
Calor específico da água: 4,2 J/(g °C)
a) De acordo com gráfico apresentado, pode-se identificar que, com o aumento na temperatura de 1°C a 3°C, ocorre diminuição do volume da água, como ilustrado a seguir.
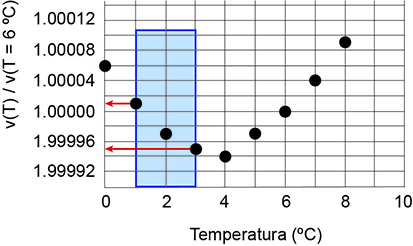
Portanto, pode-se concluir que a altura da coluna de água diminui.
b) Considerando a faixa de temperatura de 6°C a 9°C, e que o volume de 1 g de água, a 6°C, seja 1 cm3, pode-se identificar a variação no volume da água, como apresentado abaixo.
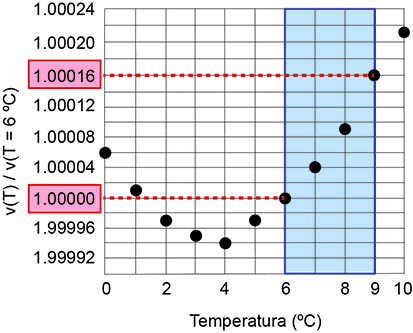
Como a altura da coluna de água a 6°C é 700 m e, o volume correspondente a 1 g, nessa temperatura, é
1 cm3, pode-se determinar a área considerada, em cm2:
Como toda a expansão volumétrica ocorre na direção vertical, é possível considerar a área da base como sendo constante. Portanto:
c) Considerando o item anterior, pode-se determinar o volume da coluna de água:
De acordo com a expressão do calor sensível, pode-se determinar o calor absorvido por unidade de área:
Por meio da expressão da definição de densidade média (), tem-se:
Substituindo-se a expressão do volume de um cilindro e fazendo-se as devidas substituições numéricas: