Duas esferas de massa M, ambas carregadas eletricamente com a mesma carga q, estão localizadas nas extremidades de fios isolantes, de comprimento L, presos ao teto, e formam o arranjo estático mostrado na figura.
a) Na folha de respostas, faça um diagrama de corpo livre da esfera 1, indicando todas as forças que atuam sobre ela.
b) Determine a razão q2/m em termos do comprimento L dos fios, da aceleração da gravidade g e da constante eletrostática do vácuo k.
c) Considere que as mesmas esferas são desconectadas dos fios e conectadas às extremidades de uma mola de constante elástica igual a 50 N/m. O conjunto é deixado sobre uma superfície isolante e sem atrito, atingindo o equilíbrio quando a força elétrica entre elas é de 0,1 N. Nessas condições, qual será o valor da energia armazenada na mola?
Note e adote:
Despreze as dimensões das esferas frente ao comprimento dos fios.
a) As forças aplicadas na esfera 1 estão indicadas no diagrama de corpo livre a seguir:
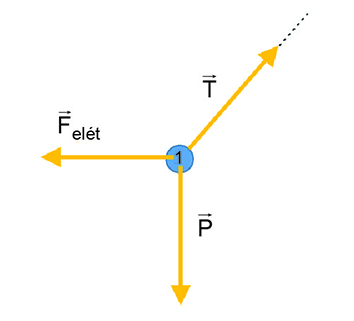
Em que:
: peso aplicado pela Terra sobre a esfera 1;
: força elétrica aplicado pela esfera 2 sobre a esfera 1;
: tração aplicada pelo fio sobre a esfera 1.
b) Como as esferas estão em equilíbrio, temos, para a esfera 1:
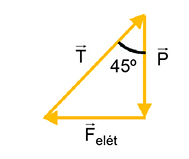
Da figura anterior:
(1)
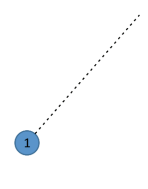
Em que “d” é a distância entre as esferas, determinada a partir da figura a seguir:
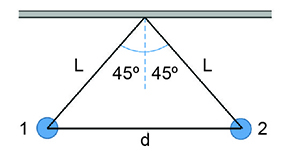
Da figura:
(2)
Dessa forma, substituindo (2) em (1):
c) Na condição de equilíbrio apresentada, a força elétrica aplicada em uma das esferas é equilibrada pela força elástica. Assim,
A energia potencial elástica armazenada na mola é dada por: