Uma bola de borracha de massa m = 50 gramas é abandonada do repouso, a partir de uma certa altura h. A resistência do ar não é desprezível, e o movimento da bola durante 0,6 segundo após o início da queda é registrado por uma câmera de alta resolução. Considerando o esquema da situação inicial e os gráficos da dependência temporal da altura y e da velocidade vertical vy da bola, responda às questões a seguir.
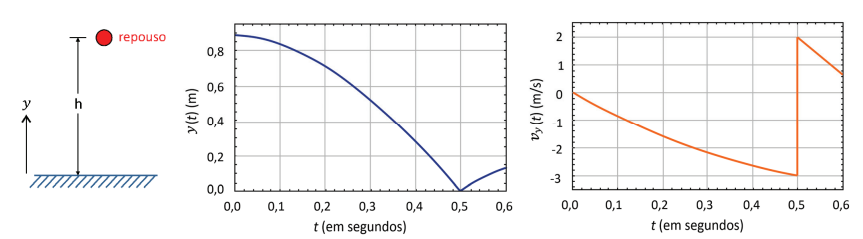
a) No instante t = 0,2 s, a força resultante que atua sobre a bola tem sentido para cima, sentido para baixo ou tem intensidade nula? Justifique sua resposta.
b) Calcule a energia cinética perdida pela bola entre os instantes imediatamente antes e imediatamente depois do choque com o solo.
c) Calcule o módulo da força média de resistência do ar atuando sobre a bola entre o instante inicial e o instante imediatamente antes de ela atingir o solo pela primeira vez.
Note e adote:
Despreze as dimensões da bola frente à altura inicial.
Aceleração da gravidade: g = 10 m/s2.
a) Analisando o gráfico da velocidade Vy no instante t = 0,2 s, podemos observar que o sinal de Vy é negativo e seu módulo aumenta. Assim, podemos concluir que a velocidade é para baixo (contra a orientação da trajetória) e o movimento é acelerado. Dessa forma, podemos afirmar que a aceleração apresenta módulo não nulo e seu sentido é o mesmo da velocidade, ou seja, para baixo. De acordo com o princípio fundamental da dinâmica, a aceleração e a resultante sempre apresentam a mesma direção e sentido, portanto, a resultante também será para baixo.
b) De acordo com o gráfico de Vy, o intervalo de tempo que dura o choque da bola com o solo é desprezível, a velocidade imediatamente antes do choque é - 3 m/s e imediatamente depois 2 m/s.
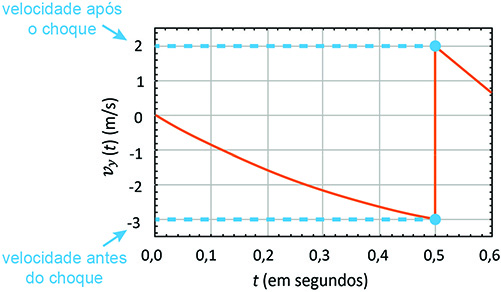
A energia cinética perdida (Ep) pode assim ser calculada:
c) A figura a seguir indica as forças aplicadas na bola, durante sua queda.
![]()
De acordo com o gráfico, o instante no qual a bola colide com o solo é t = 0,5 s. Assim, o intervalo de tempo entre o instante inicial e o instante que a bola se choca com o solo é ∆t = 0,5 s. Aplicando o teorema do impulso para esse intervalo de tempo:
Utilizando a orientação da trajetória dada (para cima), temos: