A conversão de energia mecânica das ondas do mar é uma promissora fonte alternativa de energia limpa, e vários protótipos têm sido desenvolvidos para este fim. Uma das possíveis aplicações é o uso de câmaras de ar pressurizadas que usem a oscilação das ondas do mar para fazer girar o eixo de um dínamo ou de uma turbina, gerando energia elétrica.
Considere o esquema mostrado na figura: uma boia flutua no mar e seu movimento vertical faz mover o pistão 1 de área A que comprime o ar em uma câmara pressurizada a uma pressão P0. A distância máxima entre o pistão 1 e o topo da câmara é L. Um segundo pistão (pistão 2) de área A/10 colocado horizontalmente na lateral superior da câmara é acoplado a um mecanismo que faz girar um dínamo.
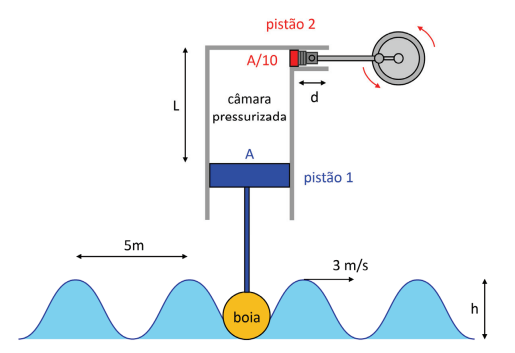
Considere inicialmente que ambos os pistões são livres para se movimentarem sem atrito e que a pressão e a temperatura do gás no interior da câmara não se alterem significativamente.
a) Se as ondas do mar forem ondas perfeitamente harmônicas com velocidade de 3 m/s e a distância entre as cristas for de 5 m, calcule o período de rotação do dínamo.
b) Se a amplitude das ondas do mar é h, calcule a distância horizontal máxima d percorrida pelo pistão 2. Considere agora uma situação em que o gerador é desativado, travando-se o pistão 2, de modo que ele não possa se mover.
c) Calcule a pressão máxima na câmara considerando que a temperatura do gás em seu interior não varie. Expresse sua resposta em termos da pressão inicial na câmara P0, e de L e h.
Note e adote:
Considere o gás no interior da câmara como sendo ideal e em equilíbrio termodinâmico em todas as etapas do processo.
a) Inicialmente, é possível determinar o período (T) da onda por meio da equação fundamental da ondulatória:
De acordo com a figura apresentada, o período de oscilação da boia coincide com o período de rotação do dínamo. Portanto:
b) Uma vez que h foi designado como sendo a amplitude da onda, pode-se concluir que o pistão 1 se desloca essa medida. Como, de acordo com o enunciado, a pressão e a temperatura do gás no interior da câmara não se alteram significativamente, o volume do gás também se mantém constante. Assim sendo, o gás passa a atuar como um elemento incompressível e, dessa maneira, a variação do volume do pistão 1 deve coincidir com a variação de volume do pistão 2. Considerando a expressão do volume do cilindro:
c) Como o pistão 2 não pode se mover, a quantidade de gás não se altera dentro da câmara. De acordo com a equação geral dos gases, pode-se concluir que a pressão máxima ocorre quando o volume ocupado pelo gás é o menor possível:
T = constante
Considerando a situação apresentada, o menor volume do gás ocupado pelo gás ocorre quando o pistão 1 possui o máximo deslocamento h (sendo a altura do cilindro nesse caso L – h):