Diversos processos celulares presentes no corpo humano envolvem fenômenos elétricos. Um dos mais importantes é o fato de uma membrana celular, que separa o interior celular do exterior, apresentar um acúmulo de ânions (cargas negativas) e cátions (cargas positivas) nas superfícies interna e externa, respectivamente, o que resulta no surgimento de uma diferença de potencial U ao longo da membrana. Considere que U cresce linearmente de 0 a U0 na região entre x = 0 e x = d, como mostra a figura.
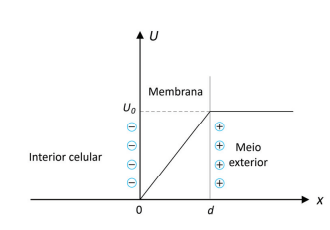
a) Indique o sentido do vetor campo elétrico no interior da membrana (se está apontando para o interior ou para o exterior da célula). Justifique sua resposta.
b) Obtenha o módulo do campo elétrico (em V/m) considerando que a membrana tenha espessura d = 64 e que U0 = 0,08 V.
c) Supondo agora uma membrana em que o campo elétrico tenha intensidade 107 V/m, encontre a razão Fe/Fg, em que Fe é o módulo da força eletrostática e Fg é o módulo da força gravitacional, ambas exercidas sobre um íon monovalente localizado na região 0<x<d, conforme a figura.
FNote e adote:
1 = 10−10 m
Carga de um íon monovalente = 1,6 × 10−19 C.
Considere, para efeitos de cálculo desta questão, a massa de um íon como 10−30 kg.
Aceleração da gravidade: g = 10m/s2.
a) O vetor campo elétrico está apontando para o interior da célula, pois seu sentido sempre é para a região de menor potencial elétrico.
b) De acordo com o texto e com o gráfico, a d.d.p. (U) cresce linearmente entre o meio interior e exterior. Dessa forma, podemos afirmar que o campo elétrico no interior da membrana é uniforme, logo:
c) Sendo o íon monovalente, sua carga é . Logo, podemos calcular a relação pedida da seguinte maneira: