Considere, no plano cartesiano, a circunferência com centro no ponto (0, 3) e com raio 2 e, para cada a ∈ começar estilo tamanho matemático 14px reto números reais fim do estilo, a ≠ 0, a parábola cuja equação é y = ax2 + 1.

a) Para a = −1, encontre o ponto comum entre a circunferência e a parábola.

b) Para a = 1, apresente 3 pontos em comum entre a circunferência e a parábola.

c) Encontre todos os valores de a para os quais a circunferência e a parábola possuam exatamente 3 pontos em comum.

Observe a seguinte figura, que mostra a circunferência e o feixe de parábolas que passam pelo ponto (0,1):

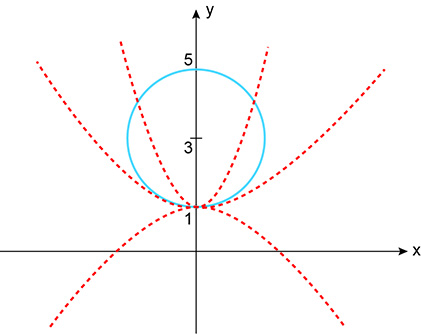
a) Com a < 0, a parábola possui concavidade no sentido contrário ao do eixo y e, portanto, da figura anterior, o ponto de intersecção é (0,1). 

b) A equação da circunferência é dada por começar estilo tamanho matemático 14px reto x ao quadrado espaço mais espaço parêntese esquerdo reto y espaço menos espaço 3 parêntese direito ao quadrado espaço igual a espaço 4 fim do estilo. Com a = 1, os pontos em comum são as soluções do sistema:

começar estilo tamanho matemático 14px abre chaves atributos de tabela alinhamento de coluna left fim dos atributos linha com célula com reto x ao quadrado espaço mais espaço estreito parêntese esquerdo reto y espaço menos espaço 3 parêntese direito ao quadrado espaço igual a espaço 4 fim da célula linha com célula com reto y espaço igual a espaço reto x ao quadrado espaço mais espaço 1 fim da célula fim da tabela fecha fim do estilo

Da segunda equação, tem-se x2 = y - 1 e, substituindo na primeira, vem:

começar estilo tamanho matemático 14px reto y espaço menos espaço 1 espaço mais espaço parêntese esquerdo reto y espaço menos espaço 3 parêntese direito ao quadrado espaço igual a espaço 4 reto y espaço menos espaço 1 espaço mais espaço reto y ao quadrado espaço menos espaço 6 reto y espaço mais espaço 9 espaço igual a espaço 4 reto y ao quadrado espaço menos espaço 5 reto y espaço mais espaço 4 espaço igual a espaço 0 fim do estilo

Resolvendo essa equação, obtém-se y = 1 ou y = 4. Como x2 = y - 1, então se y = 1, tem-se x2 = 1 - 1 e, portanto, x = 0; se y = 4, tem-se x2 = 4 - 1 e, portanto, x = ±começar estilo tamanho matemático 14px raiz quadrada de 3 fim do estilo.

Assim, os 3 pontos pedidos são (0, 1), (começar estilo tamanho matemático 14px raiz quadrada de 3 fim do estilo, 4) e (-começar estilo tamanho matemático 14px raiz quadrada de 3 fim do estilo, 4).

c) Considere o sistema:

começar estilo tamanho matemático 14px abre chaves atributos de tabela alinhamento de coluna left fim dos atributos linha com célula com reto x ao quadrado espaço mais espaço parêntese esquerdo reto y espaço menos espaço 3 parêntese direito ao quadrado espaço igual a espaço 4 fim da célula linha com célula com reto y espaço igual a espaço ax ao quadrado espaço mais espaço 1 fim da célula fim da tabela fecha fim do estilo

Da segunda equação, tem-se x2 = começar estilo tamanho matemático 14px numerador reto y menos 1 sobre denominador reto a fim da fração fim do estilo e, substituindo na primeira, vem:

começar estilo tamanho matemático 14px numerador reto y espaço menos espaço 1 sobre denominador reto a fim da fração espaço mais espaço estreito parêntese esquerdo reto y espaço menos espaço 3 parêntese direito ao quadrado espaço igual a espaço 4 fim do estilo

começar estilo tamanho matemático 14px reto y espaço menos espaço 1 espaço mais espaço reto a parêntese esquerdo reto y ao quadrado espaço menos espaço 6 reto y espaço mais espaço 9 parêntese direito espaço igual a espaço 4 reto a fim do estilo

começar estilo tamanho matemático 14px ay ao quadrado espaço mais espaço parêntese esquerdo 1 espaço menos espaço 6 reto a parêntese direito reto y espaço mais espaço parêntese esquerdo 5 reto a espaço menos espaço 1 parêntese direito espaço igual a espaço 0 fim do estilo

Uma das raízes dessa equação é y = 1, pois a ∙ 12 + (1 - 6a) ∙ 1 + (5a - 1) = 0, o que significa que um ponto em comum é (0,1).

Para que haja somente outros dois pontos de intersecção, a outra raiz da equação anterior deve estar entre 1 e 5. 

Dado que uma das raízes vale 1 e o produto das raízes vale começar estilo tamanho matemático 14px numerador 5 reto a menos 1 sobre denominador reto a fim da fração fim do estilo, então a outra raiz também é dada por começar estilo tamanho matemático 14px numerador 5 reto a menos 1 sobre denominador reto a fim da fração fim do estilo. Assim:

1 < começar estilo tamanho matemático 14px numerador 5 reto a menos 1 sobre denominador reto a fim da fração fim do estilo < 5

a < 5a - 1 < 5a

Da relação anterior, tem-se:

  • a < 5a - 1, o que implica -4a < -1 e, portanto, a > começar estilo tamanho matemático 14px 1 quarto fim do estilo;
  • 5a - 1 < 5a, o que implica 0a < 1 e, portanto, a ∈ começar estilo tamanho matemático 14px reto números reais com mais subscrito com asterisco sobrescrito fim do estilo.

Logo, a > começar estilo tamanho matemático 14px 1 quarto fim do estilo.