Uma pirâmide P tem base quadrada A0B0C0D0 de lado medindo 1u . m apoiada em um plano Π, e quatro faces que são triângulos equiláteros, ligando a base ao ápice E0 de de P. Os dezesseis pontos A1, A2, A3, B1, B2, B3, C1, C2, C3, D1, D2, D3, E1, E2, E3 e E4, indicados na figura, dividem cada aresta da pirâmide em três segmentos de igual medida.
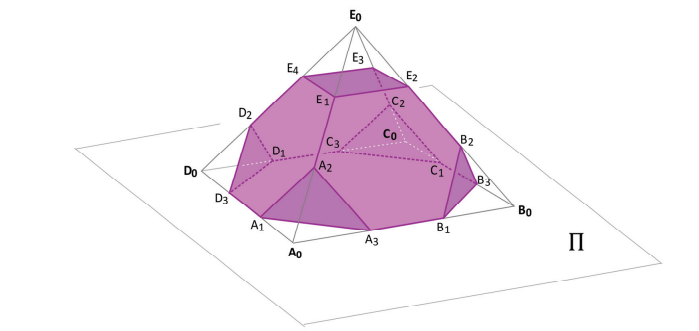
Um novo sólido S, em destaque na figura, é produzido subtraindo-se de P as cinco pirâmides A0A1A2A3, B0B1B2B3,C0C1C2C3, D0D1D2D3, E0E1E2E3E4. Determine:
a) o perímetro da face de S que se apoia em Π, cujos vértices são A1, A3, B1, B3, C1, C3, D1 e D3.
b) o volume de S.
c) a distância entre A1 e E2.
a) Do enunciado, tem-se que e
. No triângulo retângulo
, tem-se
, e, pelo teorema de Pitágoras, vem:
Portanto, o perímetro da face pedido vale
b) O apótema da pirâmide é igual à altura de um triângulo equilátero cujo lado mede 1 u.m. e vale
. Como o apótema da base dessa pirâmide mede
, então a altura h dessa pirâmide é tal que
e, assim,
Logo, o volume dessa pirâmide vale
.
O volume de S pode ser obtido fazendo-se o volume da pirâmide menos os volumes das pirâmides (congruentes)
,
,
e
e menos o volume da pirâmide
.
A área do triângulo retângulo vale
; como
, então, pelo teorema de Tales, a distância de A2 ao plano
é
da distância de
ao plano
, que vale
. Logo, a altura da pirâmide
vale
, e, assim, seu volume vale
.
A pirâmide é semelhante à pirâmide
com razão de semelhança igual a
; assim, seu volume é
do volume da pirâmide
e vale
.
Portanto, o volume de S é igual a .
c) Observe-se a figura:
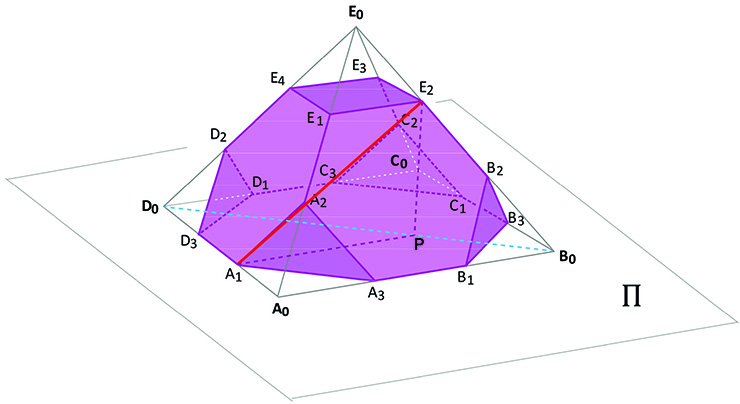
Como , então, pelo teorema de Tales, a distância de E2 ao plano
é de
da distância de E0 ao plano
, que vale
Assim,
Além disso, como
, então como consequência do teorema de Tales tem-se
.
Aplicando o teorema de Pitágoras no triângulo retângulo , vem: