Considere o conjunto C de pontos do plano cartesiano da forma (m, n), com m e n pertencentes a {3, 4, 5, 6, 7, 8, 9}.
a) Apresente todos os pontos (m, n) de C para os quais o produto m . n é maior do que 60.
b) Sorteando-se um ponto (m, n) de C, com iguais probabilidades para todos os pontos, qual é a probabilidade de que a fração e seja redutível?
c) Sorteando-se, com iguais probabilidades, dois pontos distintos de C, qual é a probabilidade de que a distância entre eles seja igual a ?
Note e Adote:
Uma fração é redutível quando m e n possuem um divisor natural em comum, além do 1.
a) Para que o produto seja maior que 60, é necessário que pelo menos um dos números m ou n seja maior que 6, pois 6∙9 < 60. Assim, os pares em que isso ocorre são (7, 9), (8, 8), (8, 9), (9, 7), (9, 8), (9, 9).
b) Dos 7∙7 = 49 pontos de C, aqueles em que o par (m, n) é redutível, ou seja, mdc(m, n) > 1, são:
(3, 3), (3, 6), (3, 9), (4, 4), (4, 6), (4, 8), (5, 5), (6, 3), (6, 4), (6, 6), (6, 8), (6, 9), (7, 7), (8, 4), (8, 6), (8, 8), (9, 3), (9, 6), (9, 9).
Assim, a probabilidade pedida vale .
c) Para que a distância entre dois pontos seja igual a , deve-se ter (∆x)2 + (∆y)2 = 13. Como os pontos de C têm coordenadas inteiras, as únicas possibilidades inteiras para ∆x e ∆y são ∆x = ± 2 e ∆y = ± 3 ou ∆x = ± 3 e ∆y = ± 2. Analisando cada caso, tem-se:
1º caso: ∆x = ± 2 e ∆y = ± 3
Observe-se a tabela a seguir:
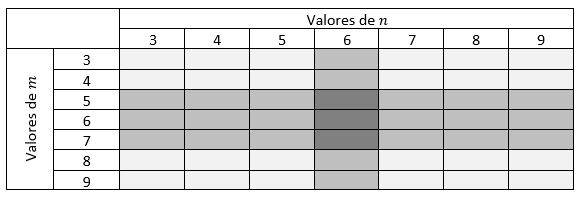
Todos os pares ordenados formados por valores de m e n pertencentes à região cinza clara possuem somente 1 outro par de C que satisfaz ∆x=± 2 e ∆y = ± 3 (por exemplo, em relação ao par (3, 3). Essa condição só é satisfeita por (5, 6)); já os pares cujos valores de m e n pertencem à região cinza ‘médio’ são os únicos que possuem somente 2 outros pares de C que satisfazem ∆x = ± 2 e ∆y = ± 3 (por exemplo, em relação ao par (4, 6). Essa condição só é satisfeita por (6, 9) e (6, 3)); por fim, os pares cujos valores de m e n pertencem à região cinza escura são os únicos que possuem somente 4 outros pares de C que satisfazem ∆x = ± 2 e ∆y = ± 3 (por exemplo, em relação ao par (5, 6). Essa condição só é satisfeita por (7, 9), (3, 9), (7, 3) e (5, 3)).
Como é possível escolher dois pontos distintos de C de 49∙48 maneiras, a probabilidade de ocorrer o 1º caso vale (I).
2º caso: ∆x = ± 3 e ∆y = ± 2
Observe-se a tabela a seguir:
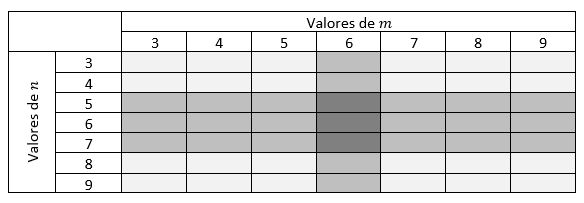
Como essa tabela pode ser obtida fazendo-se a transposta da anterior, então a probabilidade de ocorrência desse 2º caso também vale (II).
De (I) e (II), tem-se que a probabilidade pedida vale .