Uma função f está definida no intervalo [−2, 9] da seguinte forma: para x ∈ [−2 , 2], f leva x em x2 e, no restante do domínio, o seu gráfico é formado por dois segmentos de reta conforme mostra a figura.
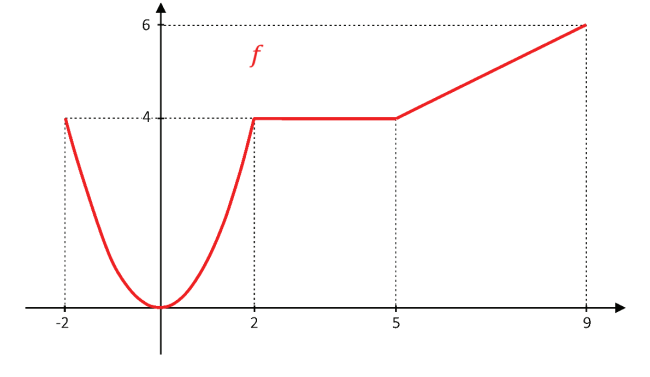
a) Apresente todos os intervalos do domínio da função f nos quais ela é crescente.
b) Determine os valores de f nos pontos .
c) Para cada valor de x ∈ ]0 , 9[ , considere o retângulo Rx com vértices nos pontos A = (x , 0), B = (9 , 0), C = (9 , f(x)) e D = (x, f(x)). Escreva a expressão da área de Rx, em função de x, para x no intervalo ]0 , 9[.
a) Entendendo a pergunta como os intervalos do domínio em que a função é estritamente crescente, tem-se que a resposta são todos os subintervalos contidos na união dos intervalos [0, 2] e [5, 9].
b) (pois,
)
(pois,
)
No intervalo [5, 9], tem-se y – 4 = m (x – 5), com .
Logo, nesse intervalo, e, portanto,
.
Resposta:
c)
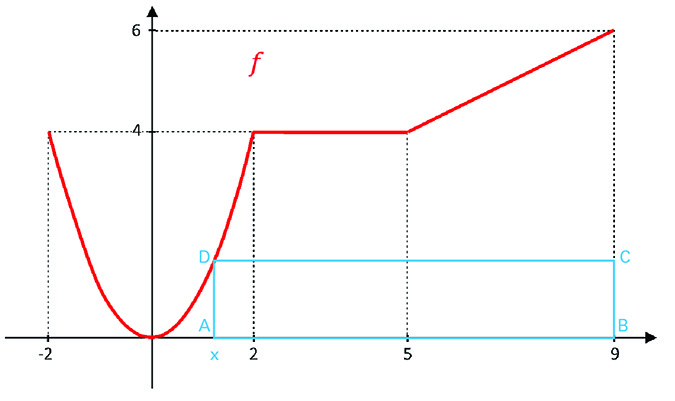
A medida da base do retângulo é dada por AB = 9 – x, e sua altura é dada por h = f(x).
No intervalo ]0, 2], tem-se h = x2, logo a área Rx é dada por Rx = (9 – x) x2, isto é Rx = 9x2 – x3;
No intervalo ]2, 5], tem-se h = 4, logo a área Rx é dada por Rx = (9 – x) (4), isto é Rx = 36 – 4x;
No intervalo ]5, 9[, tem-se , logo a área Rx é dada por Rx =
.