O inversor de Peaucellier é um mecanismo articulado, inventado no século XIX, que permite transformar movimento retilíneo em movimento circular. O mecanismo é composto por seis barras articuladas e um ponto fixo, conforme mostra a figura.
Na figura 1, P é o ponto fixo do mecanismo, A, B, C e D são as quatro articulações, que são pontos móveis, ABCD é um losango e PA = PC. A figura 2 mostra um inversor de Peaucellier em que são diagonais do quadrilátero PABC, PA = PC = 10 cm, BD = 12 cm e M é ponto médio de
.
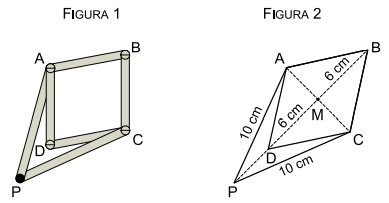
Sendo PD = x e AM = y, ambos em centímetros, no sistema cartesiano de eixos ortogonais Oxy, origem O(0, 0) e semieixo positivo Ox contendo a diagonal , o gráfico da equação que relaciona x e y é uma
Como ABCD é losango, suas diagonais são perpendiculares. Assim, aplicando o teorema de Pitágoras no triângulo retângulo AMP, tem-se:
PM2 + AM2 = AP2
(x + 6)2 + y2 = 102
Se x e y fossem números reais quaisquer, a representação geométrica da equação (x + 6)2 + y2 = 102 no plano cartesiano Oxy seria uma circunferência cujo centro é o ponto (-6, 0) e raio medindo 10 cm. No entanto, como x e y representam medidas de segmentos, então x, y > 0 de modo que a representação geométrica é um arco dessa circunferência, contendo somente os pontos dela que estão no 1º quadrante.
Portanto, a questão não possui uma alternativa correta.