Em um recipiente de paredes rígidas, estão confinados 4 mols de um gás monoatômico ideal que, ao absorver determinada quantidade de calor, sofreu uma transformação isovolumétrica entre dois estados, I e II, representada no diagrama P × V.
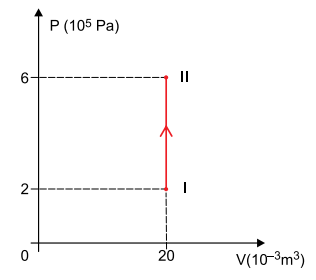
Adotando os valores para a constante universal dos gases e
para o calor específico molar desse gás a volume constante, a quantidade de calor absorvida pelo gás para que sofresse tal transformação foi de
Uma vez que, do estado I ao estado II, o volume se manteve constante, a transformação é isométrica.
Neste caso, o trabalho da força de pressão do gás é nulo e, pela primeira lei da Termodinâmica, a variação de energia interna se deve, exclusivamente, às trocas de calor entre o gás e o meio.
Algebricamente:
Por se tratar de um gás monoatômico e ideal, a variação de energia interna é dada por:
Uma vez que , temos: