Uma pessoa comprou uma caneca para tomar sopa, conforme ilustração.
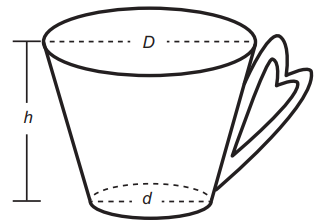
Sabe-se que 1 cm3 = 1 mL e que o topo da caneca é uma circunferência de diâmetro (D) medindo 10 cm, e a base é um círculo de diâmetro (d) medindo 8 cm. Além disso, sabe-se que a altura (h) dessa caneca mede 12 cm (distância entre o centro das circunferências do topo e da base).
Utilize 3 como aproximação para π.
Qual é a capacidade volumétrica, em mililitro, dessa caneca?
Considere a figura a seguir, em que foram construídos dois cones semelhantes entre si a partir do tronco que corresponde ao formato da caneca.
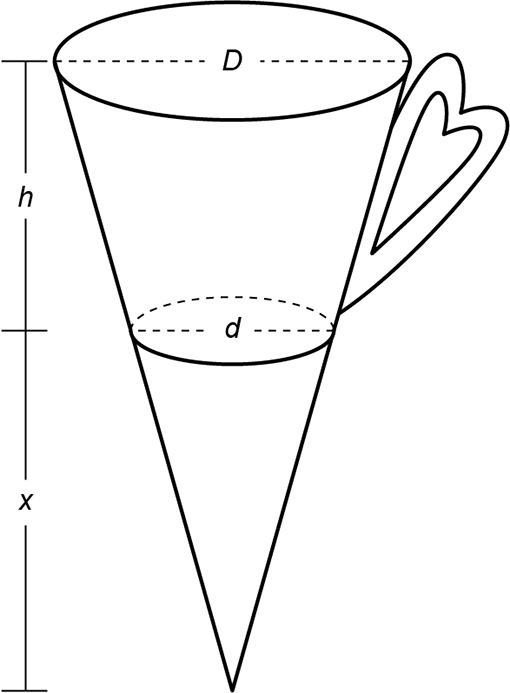
Da figura, tem-se:
Assim, o cone maior possui altura igual a x + 12, ou seja, 60 cm, e raio da base de medida 5 cm.
Já a altura do cone menor é x, ou seja, 48 cm, e seu raio da base mede 4 cm.
Logo, o volume “V” da caneca, em cm3, é dado pela diferença entre o volume do cone maior e o volume do cone menor:
Como 1 cm3 = 1 mL, a capacidade volumétrica da caneca é de 732 mL.