O instrumento de percussão conhecido como triângulo é composto por uma barra fina de aço, dobrada em um formato que se assemelha a um triângulo, com uma abertura e uma haste, conforme ilustra a Figura 1.
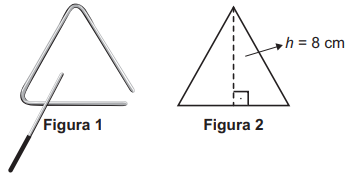
Uma empresa de brindes promocionais contrata uma fundição para a produção de miniaturas de instrumentos desse tipo. A fundição produz, inicialmente, peças com o formato de um triângulo equilátero de altura h, conforme ilustra a Figura 2. Após esse processo, cada peça é aquecida, deformando os cantos, e cortada em um dos vértices, dando origem à miniatura. Assuma que não ocorram perdas de material no processo de produção, de forma que o comprimento da barra utilizada seja igual ao perímetro do triângulo equilátero representado na Figura 2.
Considere 1,7 como valor aproximado para .
Nessas condições, o valor que mais se aproxima da medida do comprimento da barra, em centímetro, é
Sendo 2x a medida, em centímetro, do lado do triângulo equilátero, cujo formato corresponde às peças produzidas pela fundição, tem-se a figura:
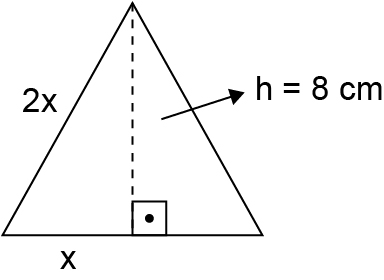
Aplicando o teorema de Pitágoras a um dos triângulos retângulos da figura:
O perímetro p desse triângulo é tal que:
Admitindo que √3 = 1,7, o perímetro vale 27,2 cm. Logo, dentre os valores apresentados nas alternativas, o que mais se aproxima do comprimento da barra, em centímetro, é 27,18.