Num octaedro regular, duas faces são consideradas opostas quando não têm arestas, nem vértices em comum. Na figura, observa-se um octaedro regular e uma de suas planificações, na qual há uma face colorida na cor cinza escuro e outras quatro faces numeradas.

Qual(is) face(s) ficará(ão) oposta(s) à face de cor cinza escuro, quando o octaedro for reconstruído a partir da planificação dada?
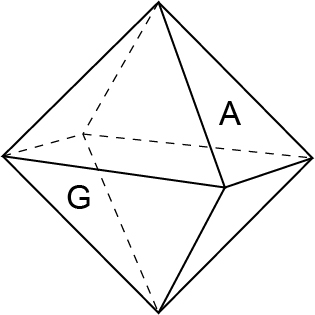
Cada face de um octaedro regular possui uma única face oposta. Por exemplo, na figura abaixo, a face A é oposta à face G.
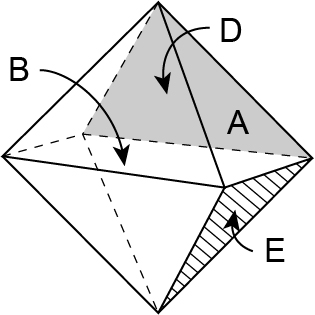
Observe ainda que a face A possui uma aresta em comum com três faces: B, D e E.
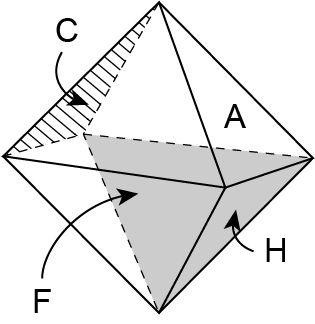
E a face A possui um vértice comum, sem possuir aresta comum, com outras três faces: C, F e H.
Considere agora a figura da planificação do octaedro regular.
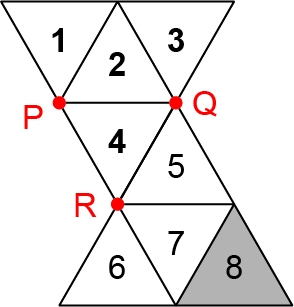
Vamos mostrar que as faces 4 e 8 (a face sombreada) são opostas.
- Há três faces com uma aresta comum com a face 4: face 2 (aresta PQ), face 5 (aresta QR) e face 6 (aresta PR). Note que, ao montar a superfície do octaedro, um dos lados da face 6 será unido a um dos lados da face 4, formando a aresta PR.
- Há três faces com um vértice comum com a face 4, mas sem aresta comum com ela: face 1 (vértice P), face 3 (vértice Q) e face 7 (vértice R).
Assim, a única face que não tem aresta nem vértice comum com a face 4 é a face 8. Portanto, a face 4 ficará oposta à face de cor cinza escuro quando o octaedro for reconstruído.