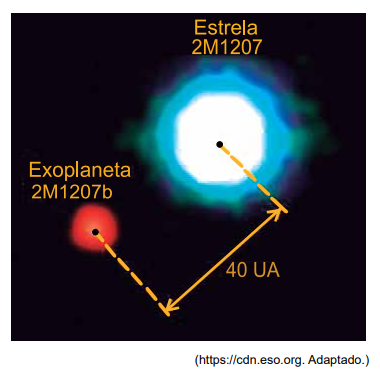
A imagem mostra o exoplaneta 2M1207b em órbita ao redor de sua estrela 2M1207 na constelação de Centauro, distantes 40 UA um do outro. Esse é o primeiro exoplaneta do qual se obteve uma imagem direta. Em comparação com objetos do sistema solar, sabe-se que esse exoplaneta tem uma massa correspondente a 5 vezes a massa do planeta Júpiter e que sua estrela tem massa igual a 0,025 vezes a massa do Sol.
Considere os seguintes dados:
Massa do Sol: 2 × 1030 kg
Massa de Júpiter: 2 × 1027 kg
1 UA: 1,5 × 1011 m
G = constante universal da gravitação = 6 × 10–11
A intensidade da força de atração gravitacional entre o exoplaneta 2M1207b e sua estrela é de, aproximadamente,
A intensidade da força de atração gravitacional entre o exoplaneta 2M1207b e sua estrela pode ser obtida pela lei da Gravitação Universal de Newton, como segue:
Em que Mexoplan = 5∙MJupiter, Mestrela = 0,025∙MSol e d = 40 uA.
Substituindo-se os valores numéricos fornecidos: