Um aplicativo instalado no celular de um ciclista informa, de 10 em 10 minutos do passeio de bicicleta, o tempo acumulado t e a distância acumulada d, em minutos e quilômetros. A tabela e o gráfico mostram os dados informados pelo aplicativo ao término de um passeio de 50 minutos. Quando o método estatístico do aplicativo identifica que o conjunto de pares ordenados (t, d) se ajusta razoavelmente bem a uma reta, ele informa sua equação que, no caso do conjunto de dados da tabela, foi d=0,311t+0,53.
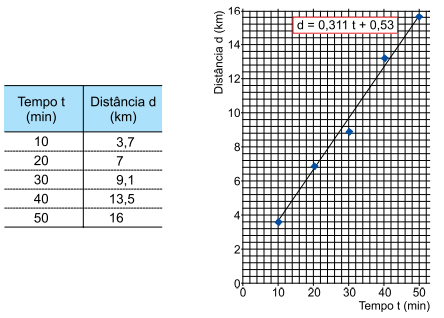
Analisando o gráfico, a equação e os cinco pares ordenados (t, d) da tabela, observa-se que a equação de reta fornecida pelo aplicativo comete erros por superestimativa ou por subestimativa no cálculo de d, para cada um dos cinco valores de t. O menor erro por superestimativa de d cometido pela equação fornecida, em termos percentuais, foi de
Utilizando a equação da reta, obtemos os seguintes valores para d e para a diferença ∆d entre ele e o valor do aplicativo:
t = 10 → d = 0,311 ∙ 10 + 0,53 ∴ d = 3,64 ⟹ ∆d = -0,06
t = 20 → d = 0,311 ∙ 20 + 0,53 ∴ d = 6,75 ⟹ ∆d = -0,25
t = 30 → d = 0,311 ∙ 30 + 0,53 ∴ d = 9,86 ⟹ ∆d = +0,76
t = 40 → d = 0,311 ∙ 40 + 0,53 ∴ d = 12,97 ⟹ ∆d = -0,53
t = 50 → d = 0,311 ∙ 50 + 0,53 ∴ d = 16,08 ⟹ ∆d = +0,08
O menor erro percentual por superestimativa é = 0,5%.