Um objeto linear AB é colocado perpendicularmente ao eixo principal de um espelho esférico convexo, a uma distância d do vértice desse espelho. A figura mostra um raio de luz (R) proveniente da extremidade A do objeto e a imagem A’ desse ponto.
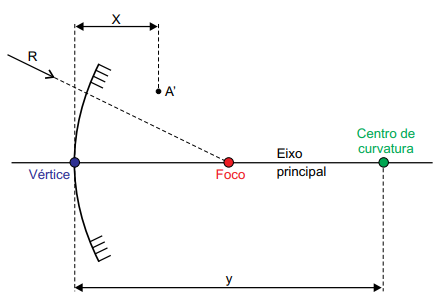
Considerando as dimensões indicadas na figura, a distância d é igual a
A partir do enunciado e da figura,
-
p = +d
-
p' = –x (imagem virtual ⇒ p’ < 0)
-
f =
(espelho convexo ⇒ f < 0)
Aplicando a equação dos pontos conjugados: