Um círculo está inscrito em um quadrilátero ABCD. Seja T o ponto de tangência do lado DA com o círculo. Sabe-se que as medidas dos lados AB, BC e CD formam, nesta ordem, uma progressão aritmética crescente de números inteiros e que a medida do lado DA é 3. Considerando que a medida do segmento TA é um número inteiro, as medidas dos lados AB, BC e CD são, respectivamente:
Como (AB, BC, CD) é uma P.A., denotando por r a razão dessa P.A., tem-se AB = BC – r e CD = BC + r. Pelo teorema de Pitot, conclui-se que:
Como a P.A. é crescente, então r > 0. A partir disso, considere a figura:
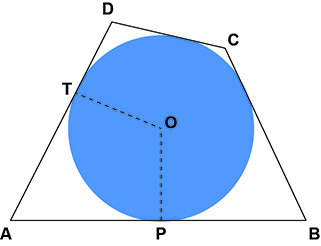
Como as medidas dos lados são números inteiros, então r = 1 (e AB = 3 – 1 = 2) ou r = 2 (e AB = 3 – 2 = 1). Dado que AT é um número inteiro e AT < 3, então AT = 1 ou AT = 2.
- Se AT = 2, como AT = AP, então AP = 2, o que é absurdo, pois AP < AB.
- Se AT = 1, como AT = AP, então AP = 1, o que é possível quando AB = 2 (pois AB > AP).
Assim, tem-se que as medidas AB, BC e CD valem 2, 3 e 4, respectivamente.