• C

    .

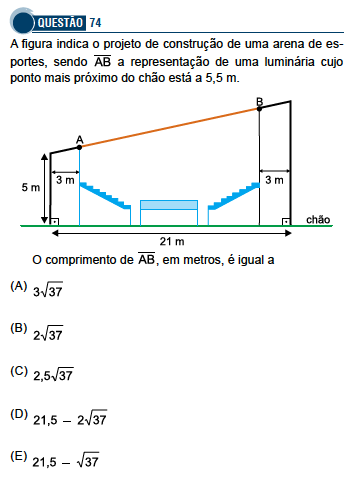
Para resolver essa questão, observe a imagem a seguir:

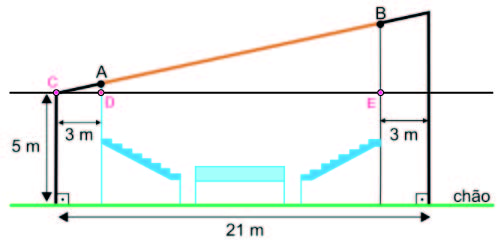
Pelo enunciado, sabe-se que a distância de A até o chão é 5,5 m. Logo AD = 0,5 m.

Aplicando o teorema de Pitágoras no triângulo ACD, tem-se que

AC2 = CD2 + AD2

∴  AC2 = 32 + começar estilo tamanho matemático 14px abre parênteses 1 meio fecha parênteses ao quadrado fim do estilo

∴  AC2 = começar estilo tamanho matemático 14px 37 sobre 4 fim do estilo

∴  AC = começar estilo tamanho matemático 14px numerador raiz quadrada de 37 sobre denominador 2 fim da fração fim do estilo

Com isso, pelo teorema de Tales, sabe-se que 

 

começar estilo tamanho matemático 14px AC sobre DC igual a AB sobre DE espaço espaço então espaço numerador começar estilo mostrar numerador raiz quadrada de 37 sobre denominador 2 fim da fração fim do estilo sobre denominador 3 fim da fração igual a numerador AB sobre denominador 21 menos 3 menos 3 espaço fim da fração espaço então espaço numerador raiz quadrada de 37 sobre denominador 6 fim da fração igual a AB sobre 15 espaço espaço então espaço AB igual a 2 vírgula 5 raiz quadrada de 37 fim do estilo

 

Observação: A questão também poderia ser resolvida usando semelhança de triângulos, obtendo a medida de começar estilo tamanho matemático 14px BC em moldura superior fim do estilo e depois retirando a medida de começar estilo tamanho matemático 14px AC em moldura superior fim do estilo.