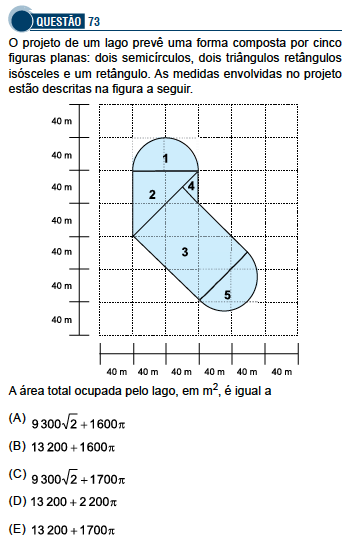
A malha quadriculada é composta por quadrados de lado com medida 40 m. Sendo assim, aplicando o teorema de Pitágoras, a diagonal d de cada quadrado destes mede .

Avaliando cada forma, tem-se que

• Figura 1:

Trata-se de um semicírculo de raio de medida 40 m. Logo, sua área, em m², é

 = 800π

• Figura 2:

Trata-se de um triângulo retângulo e isósceles de catetos de medida 80 m. Logo, sua área, em m², é

 = 3200

• Figura 4:

Trata-se de um triângulo retângulo e isósceles de hipotenusa de medida 40 m. Logo, aplicando o teorema de Pitágoras, seus catetos medem  (metade de d) e sua área, em cm², é

 = 400

• Figura 3:

Trata-se de um retângulo em que um dos lados tem medida igual a 1,5 ∙ d (isto é ) e o outro lado tem medida igual a 2 ∙ d (isto é ). Portanto, sua área, em m², é

• Figura 5:

Trata-se de um semicírculo de diâmetro de medida 1,5 ∙ d (isto é 60² m). Logo, sua área, em m², é

Somando todos os valores, tem-se que a área total ocupada pelo lago, em m², é igual a

800π + 3200 + 400 + 9600 + 900π = 13200 + 1700π