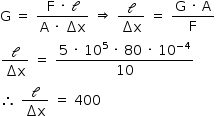Um estudo publicado em 2014 na renomada revista científica Physical Review Letters (http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.112.175502) descreve como a antiga civilização egípcia reduzia o atrito entre a areia e os trenós que levavam pedras de até algumas toneladas para o local de construção das pirâmides. O artigo demonstrou que a areia na frente do trenó era molhada com a quantidade certa de água para que ficasse mais rígida, diminuindo a força necessária para puxar o trenó. Caso necessário, use g = 10 m/s2 para resolver as questões abaixo.
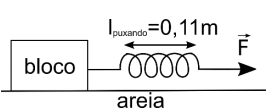
a) Considere que, no experimento realizado pelo estudo citado acima, um bloco de massa m = 2 kg foi colocado sobre uma superfície de areia úmida e puxado por uma mola de massa desprezível e constante elástica k = 840 N/m, com velocidade constante, como indica a figura ao lado. Se a mola em repouso tinha comprimento leprouso = 0,10 m, qual é o coeficiente de atrito dinâmico entre o bloco e a areia?
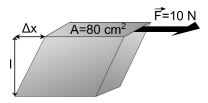
b) Neste experimento, o menor valor de coeficiente de atrito entre a areia e o trenó é obtido com a quantidade de água que torna a areia rígida ao cisalhamento. Esta rigidez pode ser caracterizada pelo seu módulo de cisalhamento, dado por G = Fl⁄A∆x, em que F é o módulo da força aplicada tangencialmente a uma superfície de área A de um material de espessura l, e que a deforma por uma distância ∆x, como indica a figura ao lado. Considere que a figura representa o experimento realizado para medir G da areia e também o coeficiente de atrito dinâmico entre a areia e o bloco, ambos em função da quantidade de água na areia. O resultado do experimento é mostrado no gráfico apresentado no espaço de resolução abaixo. Com base no experimento descrito, qual é o valor da razão l/∆x da medida que resultou no menor coeficiente de atrito dinâmico?
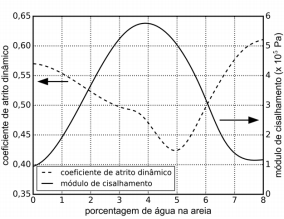
Note que há duas escalas para o eixo das ordenadas, uma para cada curva. A legenda e as setas indicam as escalas de cada curva.
a) O bloco está submetido às seguintes forças:
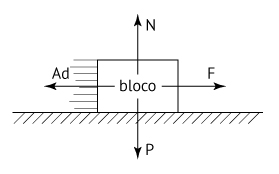
Como o bloco está em MRU, a resultante é nula. Logo, o coeficiente de atrito dinâmico pode ser assim determinado:
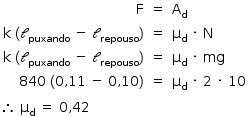
b) O módulo de cisalhamento da areia pode ser obtido, a partir do gráfico fornecido, utilizando µ = 0,42, como segue:
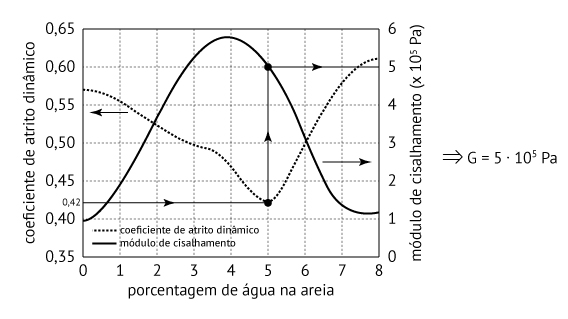
Logo, a razão ℓ/Δx pode ser assim determinada: