O Parque Güell em Barcelona é um dos mais impressionantes parques públicos do mundo e representa uma das obras mais marcantes do arquiteto Antoni Gaudí. Em sua obra, Gaudí utilizou um número imenso de azulejos coloridos.
a) Considere que, no Parque Güell, existe um número N = 2 x 106 de azulejos cujas faces estão perfeitamente perpendiculares à direção da radiação solar quando o sol está a pino na cidade de Barcelona. Nessa situação, a intensidade da radiação solar no local é I = 1200 W/m2 . Estime a área de um azulejo tipicamente presente em casas e, a partir da área total dos N azulejos, calcule a energia solar que incide sobre esses azulejos durante um tempo t = 60 s.
b) Uma das esculturas mais emblemáticas do parque Güell tem a forma de um réptil multicolorido conhecido como EL Drac, que se converteu em um dos símbolos da cidade de Barcelona. Considere que a escultura absorva, em um dia ensolarado, uma quantidade de calor Q = 3500 kJ. Considerando que a massa da escultura é m = 500 kg e seu calor específico é c = 700 J/(kg.K), calcule a variação de temperatura sofrida pela escultura, desprezando as perdas de calor para o ambiente.
a) A área estimada por azulejo quadrado será de:
A = L2
em que L ≈ 20 cm = 0,2 m
A ≈ 4 · 10–2 m2. Assim, a energia incidente pode ser calculada por:

b) A variação de temperatura fica assim determinada:
Q = m · c · Δθ
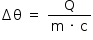
Procedendo às devidas substituições numéricas: