Plutão é considerado um planeta anão, com massa MP = 1 x 1022 kg, bem menor que a massa da Terra. O módulo da força gravitacional entre duas massas m1 e m2 é dado por 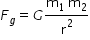 , em que r é a distância entre as massas e G é a constante gravitacional. Em situações que envolvem distâncias astronômicas, a unidade de comprimento comumente utilizada é a Unidade Astronômica (UA).
, em que r é a distância entre as massas e G é a constante gravitacional. Em situações que envolvem distâncias astronômicas, a unidade de comprimento comumente utilizada é a Unidade Astronômica (UA).
a) Considere que, durante a sua aproximação a Plutão, a sonda se encontra em uma posição que está dP = 0,15 UA distante do centro de Plutão e dr = 30 UA distante do centro da Terra. Calcule a razão 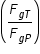 entre o módulo da força gravitacional com que a Terra atrai a sonda e o módulo da força gravitacional com que Plutão atrai a sonda. Caso necessário, use a massa da Terra MT = 6 x 1024 kg.
entre o módulo da força gravitacional com que a Terra atrai a sonda e o módulo da força gravitacional com que Plutão atrai a sonda. Caso necessário, use a massa da Terra MT = 6 x 1024 kg.
b) Suponha que a sonda New Horizons estabeleça uma órbita circular com velocidade escalar orbital constante em torno de Plutão com um raio de rP = 1 x 10−4 UA. Obtenha o módulo da velocidade orbital nesse caso. Se necessário, use a constante gravitacional G = 6 x 10−11 N.m2/kg2. Caso necessário, use 1 UA (Unidade astronômica) = 1,5 x 108 km.
a) Sendo m a massa da sonda, a razão procurada pode ser calculada como segue:
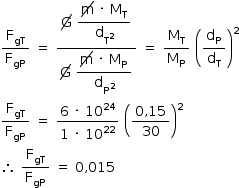
b) O movimento da sonda New Horizons é circular e uniforme. Logo, a velocidade orbital fica determinada:
