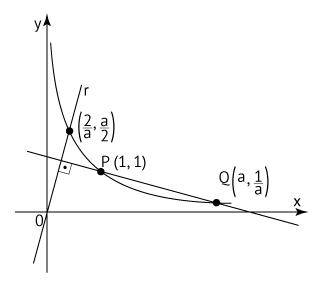
A figura abaixo exibe o gráfico da função f(x) = 1/x, definida para todo número real x > 0. Os pontos P e Q têm abscissas x = 1 e x = a, respectivamente, onde a é um número real e a > 1.
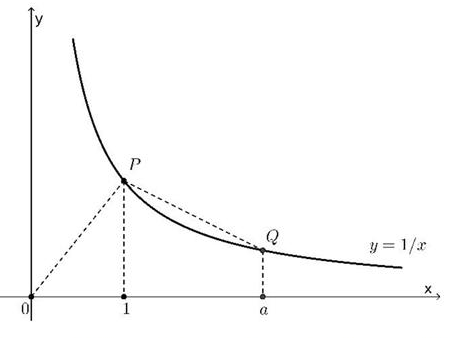
a) Considere o quadrilátero T com vértices em (0,0), P, Q e (a, 0). Para a = 2, verifique que a área de T é igual ao quadrado da distância de P a Q.
b) Seja r a reta que passa pela origem e é ortogonal à reta que passa por P e Q. Determine o valor de a para o qual o ponto de intersecção da reta r com o gráfico da função f tem ordenada y = a/2.
a)
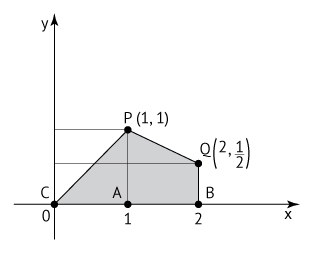
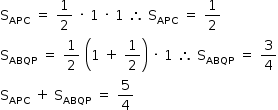

Logo, a área de T é igual ao quadrado de PQ.
b)