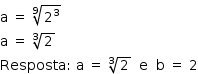Considere a função f(x) = |2x − 4| + x − 5, definida para todo número real x.
a) Esboce o gráfico de y = f(x) no plano cartesiano para −4 ≤ x ≤ 4.
b) Determine os valores dos números reais a e b para os quais a equação loga(x + b) = f(x) admite como soluções x1 = −1 e x2 = 6.
a) Do conceito de módulo, tem-se

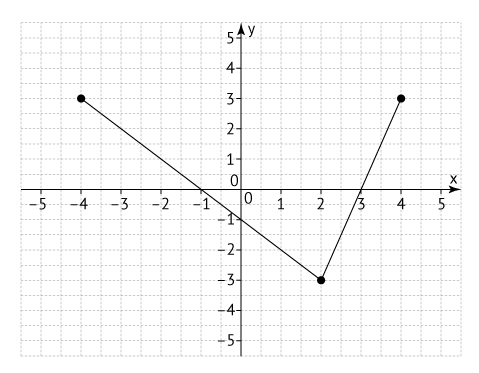
b) Para que x1 = –1 e x2 = 6 sejam soluções da equação loga(x + b) = f(x), com a e b constantes reais, deve-ser te
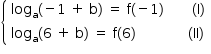
De (I) vem:
loga(–1 + b) = –(–1) – 1
loga(–1 + b) = 0
–1 + b = ao
–1 + b = 1
b = 2
Substituindo b = 2 em (II) vem:
loga(6 + 2) = 3 · 6 – 9
loga8 = 9
a9 = 8