Duas polias circulares, I e II, de raios respectivamente iguais a 30 cm e 20 cm estão apoiadas sobre uma mesa horizontal e são acopladas como mostra a figura. Na superfície da polia II está desenhada uma seta vermelha, inicialmente na posição indicada. A polia I é fixa na mesa e não gira, mas a polia II pode girar no sentido horário em torno do seu próprio centro e, simultaneamente, em torno do centro da polia I sem perder contato e sem escorregar em relação a ela. Dessa forma, o centro da polia II percorre a trajetória circular tracejada indicada na figura, que mostra uma visão superior das polias.
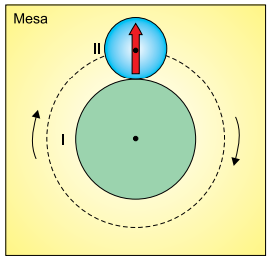
Quando a polia II der uma volta completa em torno de I e retornar à posição inicial indicada na figura, a seta em sua superfície estará na posição:
A razão entre os comprimentos da periferia das duas polias é:
Como não há escorregamento, para que um ponto na periferia da polia II complete uma volta em torno da polia I, é necessário que a polia II execute 1,5 volta em torno do seu próprio eixo.
O eixo de rotação da seta é o mesmo da polia II. Dessa forma, a seta vermelha também executará 1,5 volta. Portanto, quando a polia II retornar à posição inicial indicada na figura, a seta vermelha estará na posição indicada na alternativa B.