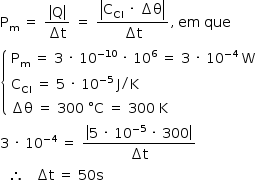Em um circuito integrado (CI), a conexão elétrica entre transistores é feita por trilhas de alumínio de 500 nm de comprimento, 100 nm de largura e 50 nm de espessura.
a) Determine a resistência elétrica de uma dessas conexões, sabendo que a resistência, em ohms, de uma trilha de alumínio é dada por R = 3 × 10–8 L/A, em que L e A são, respectivamente, o comprimento e a área da seção reta da trilha em unidades do SI.
b) Se a corrente elétrica em uma trilha for de 10 μA, qual é a potência dissipada nessa conexão?
c) Considere que um determinado CI possua 106 dessas conexões elétricas. Determine a energia E dissipada no CI em 5 segundos de operação.
d) Se não houvesse um mecanismo de remoção de calor, qual seria o intervalo de tempo Δt necessário para a temperatura do CI variar de 300 °C?

a) Utilizando-se a expressão fornecida (2ª lei de Ohm), já com as unidades:
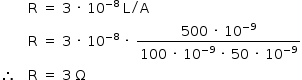
b) A potência dissipada na conexão é dada por:
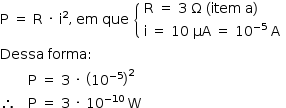
c) Aplicando-se a definição de potência média em uma conexão:
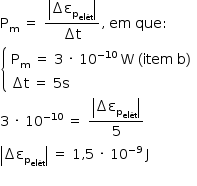
Como são 106 conexões:
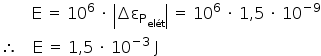
d) Aplicando-se a definição de potência média para o CI: