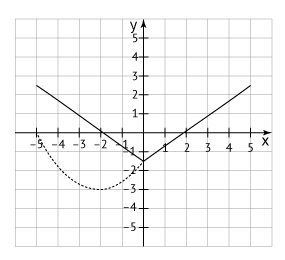
A figura abaixo representa o gráfico de uma função f: [–5,5] → ℝ. Note que f(–5) = f(2) = 0. A restrição de f ao intervalo [–5,0] tem como gráfico parte de uma parábola com vértice no ponto (–2, –3); restrita ao intervalo [0,5], f tem como gráfico um segmento de reta.
a) Calcule f(–1) e f(3).
Usando os sistemas de eixos da folha de respostas, esboce
b) o gráfico de
c) o gráfico de
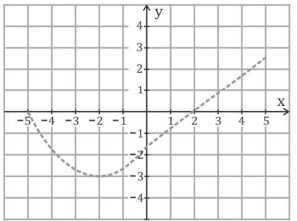
a) Para a parábola, se uma raiz é –5 e a abscissa do vértice é –2, por simetria a outra raiz é 1, assim, f (x) = a (x + 5) (x – 1) para x ∈ [ –5, 0]
De f (–2) = –3 tem-se: a · (3) (–3) = –3 
a = 
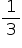e f (x) = 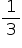(x +5) (x – 1) para x ∈ [–5, 0]
Logo, f (–1) = 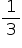· (4) (–2) f (–1) = –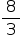
Além disso,
f (0) = 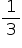· (5) (–1) f (0) = –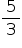
Assim, o ponto de encontro entre a reta e a parábola é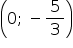 
Para x ∈ [0, 5], f (x) = mx –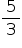
De f (2) = 0 tem-se: 0 = 2m –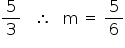 
e f (x) = 
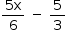para x ∈ [0, 5]
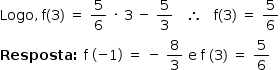
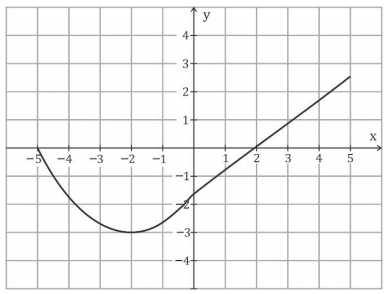
b)
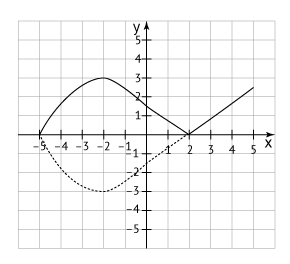
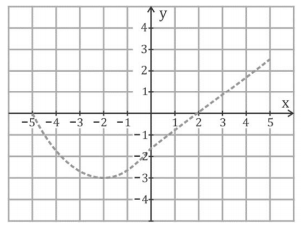
c)
