No plano cartesiano Oxy, a circunferência C tem centro no ponto P = (2, 1), e a reta t é tangente a C no ponto Q = (–1,5).
a) Determine o raio da circunferência C.
b) Encontre uma equação para a reta t.
c) Calcule a área do triângulo PQR, sendo R o ponto de interseção de t com o eixo Ox.
a) Como P = (2, 1) é o centro de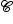 
e Q = (–1, 5) é ponto de 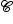, o raio r da circunferência é igual à distância entre P e Q.
Assim,
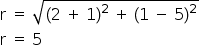
Resposta: 5
b) Como t é tangente à circunferência em Q, tem-se que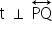 
.
Desse modo, sendo mt e mPQ os coeficientes angulares de t e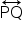 
, respectivamente, tem-se:
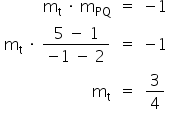
Assim, a reta t é dada pela equação
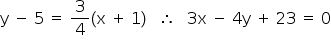
Resposta: 3x – 4y + 23 = 0
c) O ponto R é um ponto de t que tem a forma (a, 0) com a ∈ ℝ, pois R pertence ao eixo 0x.
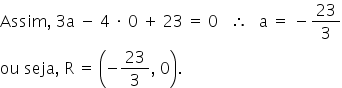
Desse modo, a área A do triângulo PQR é dada por:
Calculando o determinante D, vem:
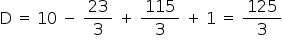
Logo
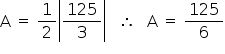
Resposta: 