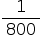João e Maria jogam dados em uma mesa. São cinco dados em forma de poliedros regulares: um tetraedro, um cubo, um octaedro, um dodecaedro e um icosaedro. As faces são numeradas de 1 a 4 no tetraedro, de 1 a 6 no cubo, etc. Os dados são honestos, ou seja, para cada um deles, a probabilidade de qualquer uma das faces ficar em contato com a mesa, após o repouso do dado, é a mesma.
Num primeiro jogo, Maria sorteia, ao acaso, um dos cinco dados, João o lança e verifica o número da face que ficou em contato com a mesa.
a) Qual é a probabilidade de que esse número seja maior do que 12?
b) Qual é a probabilidade de que esse número seja menor do que 5?
Num segundo jogo, João sorteia, ao acaso, dois dos cinco dados. Maria os lança e anota o valor da soma dos números das duas faces que ficaram em contato com a mesa, após o repouso dos dados.
c) Qual é a probabilidade de que esse valor seja maior do que 30?
a) Para que o resultado seja maior que 12, o dado escolhido tem que ser o icosaedro.
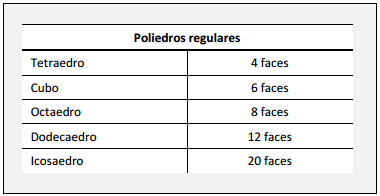
Como a probabilidade de escolher o icosaedro é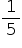 
, e a probalidade de o resultado nele ser maior que 12 é 
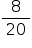, a probabilidade pedida é dada por: 
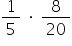, ou seja, 
.
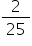Resposta: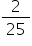
b) As probabilidades de o número ser menor que 5, em cada dado, são dadas na tabela:
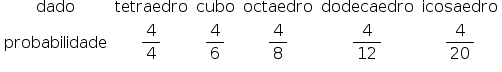
Assim, a probabilidade pedida é dada por:
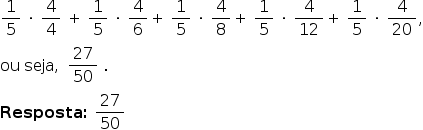
c) Para que a soma seja maior que 30, os dados escolhidos têm que ser o icosaedro e o dodecaedro. A probabilidade de que eles sejam escolhidos é
Os pares de resultados cuja soma é maior que 30 são: (20, 12), (20, 11), (19, 12).
Logo, com esses dados, a probabilidade de a soma ser maior que 30 é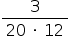 
, ou seja,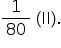 
De (I) e (II), a probabilidade pedida é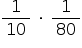 
, ou seja, 
.
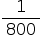Resposta: