São dadas três circunferências de raio r, duas a duas tangentes. Os pontos de tangência são P1, P2 e P3.
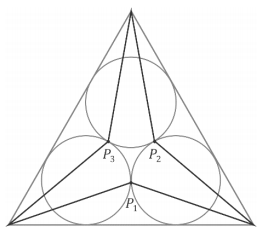
Calcule, em função de r,
a) o comprimento do lado do triângulo equilátero T determinado pelas três retas que são definidas pela seguinte exigência: cada uma delas é tangente a duas das circunferências e não intersecta a terceira;
b) a área do hexágono não convexo cujos lados são os segmentos ligando cada ponto P1, P2 e P3 aos dois vértices do triângulo T mais próximos a ele.
a)
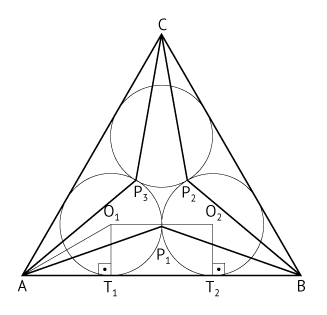

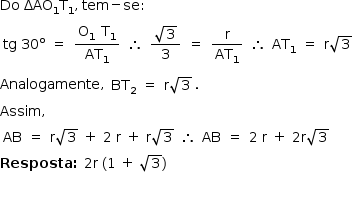
b) A área pedida pode ser calculada fazendo-se:
![«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨14px¨»«mrow»«mi»§#x000C1;rea«/mi»«mo»§#x000A0;«/mo»«mo»(«/mo»«mo»§#x02206;«/mo»«mi»ABC«/mi»«mo»)«/mo»«mo»§#x000A0;«/mo»«mo»-«/mo»«mo»§#x000A0;«/mo»«mn»3«/mn»«mo»§#x000A0;«/mo»«mo»§#x000B7;«/mo»«mi»§#x000C1;rea«/mi»«mo»§#x000A0;«/mo»«mo»(«/mo»«mo»§#x02206;«/mo»«msub»«mi»AP«/mi»«mn»1«/mn»«/msub»«mi mathvariant=¨normal¨»B«/mi»«mo»)«/mo»«mspace linebreak=¨newline¨/»«mfrac»«mrow»«msup»«mi mathvariant=¨script¨»l«/mi»«mn»2«/mn»«/msup»«mo»§#x000A0;«/mo»«msqrt»«mn»3«/mn»«/msqrt»«/mrow»«mn»4«/mn»«/mfrac»«mo»§#x000A0;«/mo»«mo»-«/mo»«mo»§#x000A0;«/mo»«mn»3«/mn»«mo»§#x000A0;«/mo»«mo»§#x000B7;«/mo»«mo»§#x000A0;«/mo»«mfrac»«mrow»«mi mathvariant=¨script¨»l«/mi»«mo»§#x000A0;«/mo»«mo»§#x000B7;«/mo»«mo»§#x000A0;«/mo»«mi mathvariant=¨normal¨»r«/mi»«/mrow»«mn»2«/mn»«/mfrac»«mo»§#x000A0;«/mo»«mo»=«/mo»«mspace linebreak=¨newline¨/»«mo»=«/mo»«mo»§#x000A0;«/mo»«mo»§#x000A0;«/mo»«mi mathvariant=¨script¨»l«/mi»«mo»§#x000A0;«/mo»«mo»§#x000B7;«/mo»«mo»§#x000A0;«/mo»«mfenced open=¨[¨ close=¨]¨»«mtable»«mtr»«mtd»«mfrac»«mrow»«mi mathvariant=¨script¨»l«/mi»«msqrt»«mn»3«/mn»«/msqrt»«/mrow»«mn»4«/mn»«/mfrac»«/mtd»«mtd»«mo»-«/mo»«/mtd»«mtd»«mfrac»«mrow»«mn»3«/mn»«mi mathvariant=¨normal¨»r«/mi»«/mrow»«mn»2«/mn»«/mfrac»«/mtd»«/mtr»«/mtable»«/mfenced»«mo»§#x000A0;«/mo»«mo»§#x000A0;«/mo»«mo»=«/mo»«mspace linebreak=¨newline¨/»«mo»=«/mo»«mo»§#x000A0;«/mo»«mn»2«/mn»«mi mathvariant=¨normal¨»r«/mi»«mo»§#x000A0;«/mo»«mfenced»«mrow»«mn»1«/mn»«mo»§#x000A0;«/mo»«mo»+«/mo»«mo»§#x000A0;«/mo»«msqrt»«mn»3«/mn»«/msqrt»«/mrow»«/mfenced»«mo»§#x000A0;«/mo»«mo»§#x000B7;«/mo»«mo»§#x000A0;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mn»2«/mn»«mi mathvariant=¨normal¨»r«/mi»«mo»§#x000A0;«/mo»«mo»(«/mo»«mn»1«/mn»«mo»§#x000A0;«/mo»«mo»+«/mo»«mo»§#x000A0;«/mo»«msqrt»«mn»3«/mn»«/msqrt»«mo»)«/mo»«mo»§#x000A0;«/mo»«mo»§#x000B7;«/mo»«mo»§#x000A0;«/mo»«mfrac»«msqrt»«mn»3«/mn»«/msqrt»«mn»4«/mn»«/mfrac»«mo»§#x000A0;«/mo»«mo»-«/mo»«mo»§#x000A0;«/mo»«mfrac»«mrow»«mn»3«/mn»«mi mathvariant=¨normal¨»r«/mi»«/mrow»«mn»2«/mn»«/mfrac»«/mrow»«/mfenced»«mo»§#x000A0;«/mo»«mo»=«/mo»«mspace linebreak=¨newline¨/»«mo»=«/mo»«mo»§#x000A0;«/mo»«mn»2«/mn»«mi mathvariant=¨normal¨»r«/mi»«mo»§#x000A0;«/mo»«mo»(«/mo»«mn»1«/mn»«mo»§#x000A0;«/mo»«mo»+«/mo»«mo»§#x000A0;«/mo»«msqrt»«mn»3«/mn»«/msqrt»«mo»)«/mo»«mo»§#x000A0;«/mo»«mo»§#x000B7;«/mo»«mo»§#x000A0;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mfrac»«mrow»«mn»2«/mn»«msqrt»«mn»3«/mn»«/msqrt»«mi mathvariant=¨normal¨»r«/mi»«/mrow»«mn»4«/mn»«/mfrac»«mo»§#x000A0;«/mo»«mo»+«/mo»«mo»§#x000A0;«/mo»«mfrac»«mrow»«mn»6«/mn»«mi mathvariant=¨normal¨»r«/mi»«/mrow»«mn»4«/mn»«/mfrac»«mo»§#x000A0;«/mo»«mo»-«/mo»«mo»§#x000A0;«/mo»«mfrac»«mrow»«mn»3«/mn»«mi mathvariant=¨normal¨»r«/mi»«/mrow»«mn»2«/mn»«/mfrac»«/mrow»«/mfenced»«mo»§#x000A0;«/mo»«mo»=«/mo»«mspace linebreak=¨newline¨/»«mo»=«/mo»«mo»§#x000A0;«/mo»«mn»2«/mn»«mi mathvariant=¨normal¨»r«/mi»«mo»§#x000A0;«/mo»«mo»(«/mo»«mn»1«/mn»«mo»§#x000A0;«/mo»«mo»+«/mo»«mo»§#x000A0;«/mo»«msqrt»«mn»3«/mn»«/msqrt»«mo»)«/mo»«mo»§#x000A0;«/mo»«mo»§#x000B7;«/mo»«mo»§#x000A0;«/mo»«mfrac»«mrow»«msqrt»«mn»3«/mn»«/msqrt»«mi mathvariant=¨normal¨»r«/mi»«/mrow»«mn»2«/mn»«/mfrac»«mo»§#x000A0;«/mo»«mo»=«/mo»«mspace linebreak=¨newline¨/»«mo»=«/mo»«mo»§#x000A0;«/mo»«msup»«mi mathvariant=¨normal¨»r«/mi»«mn»2«/mn»«/msup»«mo»§#x000A0;«/mo»«mo»(«/mo»«mn»1«/mn»«mo»§#x000A0;«/mo»«mo»+«/mo»«mo»§#x000A0;«/mo»«msqrt»«mn»3«/mn»«/msqrt»«mo»)«/mo»«mo»§#x000A0;«/mo»«mo»§#x000B7;«/mo»«mo»§#x000A0;«/mo»«msqrt»«mn»3«/mn»«/msqrt»«mo»§#x000A0;«/mo»«mo»=«/mo»«mspace linebreak=¨newline¨/»«mo»=«/mo»«mo»§#x000A0;«/mo»«msup»«mi mathvariant=¨normal¨»r«/mi»«mn»2«/mn»«/msup»«mo»§#x000A0;«/mo»«mo»(«/mo»«msqrt»«mn»3«/mn»«/msqrt»«mo»§#x000A0;«/mo»«mo»+«/mo»«mo»§#x000A0;«/mo»«mn»3«/mn»«mo»)«/mo»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨»Resposta«/mi»«mo mathvariant=¨bold¨»:«/mo»«mo»§#x000A0;«/mo»«msup»«mi mathvariant=¨normal¨»r«/mi»«mn»2«/mn»«/msup»«mo»§#x000A0;«/mo»«mo»(«/mo»«msqrt»«mn»3«/mn»«/msqrt»«mo»§#x000A0;«/mo»«mo»+«/mo»«mo»§#x000A0;«/mo»«mn»3«/mn»«mo»)«/mo»«/mrow»«/mstyle»«/math»](https://anglo.plurall.net/sites/all/libraries/ckeditor//plugins/ckeditor_wiris/integration/showimage.php?formula=cc2c80d5dc491e7b8ad7a6803b2dbcaa.png)