O nível de intensidade sonora β, em decibéis (dB), é definido pela expressão β = 10 log10 (I / I0), na qual I é a intensidade do som em W/m2 e I0 = 10-12 W/m2 é um valor de referência. Os valores de nível de intensidade sonora β = 0 e = β 120 dB correspondem, respectivamente, aos limiares de audição e de dor para o ser humano. Como exposições prolongadas a níveis de intensidade sonora elevados podem acarretar danos auditivos, há uma norma regulamentadora (NR-15) do Ministério do Trabalho e Emprego do Brasil, que estabelece o tempo máximo de 8 horas para exposição ininterrupta a sons de 85 dB e especifica que, a cada acréscimo de 5 dB no nível da intensidade sonora, deve-se dividir por dois o tempo máximo de exposição. A partir dessas informações, determine
a) a intensidade sonora ID correspondente ao limiar de dor para o ser humano;
b) o valor máximo do nível de intensidade sonora β, em dB, a que um trabalhador pode permanecer exposto por 4 horas seguidas;
c) os valores da intensidade I e da potência P do som no tímpano de um trabalhador quando o nível de intensidade sonora é 100 dB.
Note e adote:
π = 3
Diâmetro do tímpano = 1 cm
a) A partir das informações do enunciado, o limiar de dor corresponde ao nível de intensidade sonora β = 120 dB. Utilizando-se a expressão fornecida:
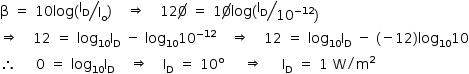
b) De acordo com o enunciado, como o tempo de exposição caiu pela metade, de 8h para 4h, o nível de intensidade sonora deverá sofrer um acréscimo de 5 dB, apresentando o valor máximo de 90 dB.
c) Sendo o nível de intensidade sonora 100 dB, tem-se:
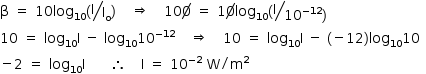
Sendo o diâmetro do tímpano d = 1 cm = 10–2 m, sua área é:
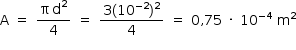
A potência P pode ser obtida pela expressão:
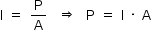
P = 10–2 · 0,75 · 10–4 = 7,5 · 10–7 W