Uma bola de bilhar, inicialmente em repouso em um ponto P, situado na borda de uma mesa de bilhar com formato circular, recebe uma tacada e se desloca em um movimento retilíneo. A bola atinge a borda no ponto R e é refletida elasticamente, sem deslizar. Chame de Q o ponto da borda diametralmente oposto a P e de θ a medida do ângulo 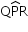 .
.
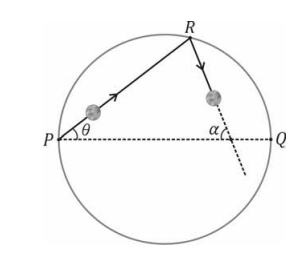
a) Para qual valor de θ, após a primeira reflexão, a trajetória da bola será paralela ao diâmetro 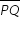 ?
?
b) Para qual valor de θ, após a primeira reflexão, a trajetória da bola será perpendicular a 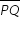 ?
?
c) Supondo agora que 30º < θ < 60º, encontre uma expressão, em função de θ, para a medida α do ângulo agudo formado pela reta que contém P e Q e pela reta que contém a trajetória da bola após a primeira reflexão na borda.
a) Note-se que, se θ = 0°, a trajetória da bola será paralela e coincidente com o diâmetro 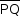 .
.
Se θ ≠ 0°, e a trajetória for paralela ao diâmetro, tem-se uma situação conforme o esboço abaixo.

Dessa forma, o ΔOPR é equilátero, isto é, θ = 60°.
Resposta: 0° ou 60°
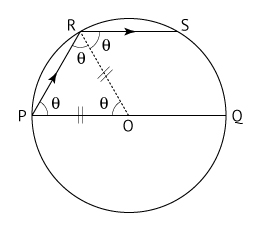
b)

Resposta: 30°
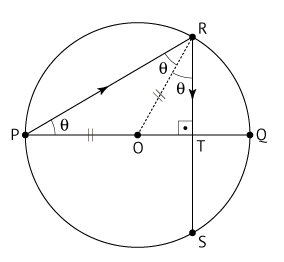
c)

Resposta: α = 180° – 3θ