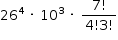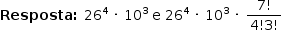Está previsto que, a partir de 1º de janeiro de 2017, entrará em vigor um sistema único de emplacamento de veículos para todo o Mercosul, o que inclui o Brasil. As novas placas serão compostas por 4 letras e 3 algarismos. Admita que no novo sistema possam ser usadas todas as 26 letras do alfabeto, incluindo repetições, e os 10 algarismos, também incluindo repetições. Admita ainda que, no novo sistema, cada carro do Mercosul tenha uma sequência diferente de letras e algarismos em qualquer ordem. Veja alguns exemplos das novas placas.

No novo sistema descrito, calcule o total de placas possíveis com o formato “Letra-Letra-Algarismo-Algarismo- -Algarismo-Letra-Letra”, nessa ordem. Em seguida, calcule o total geral de possibilidades de placas com 4 letras (incluindo repetição) e 3 algarismos (incluindo repetição) em qualquer ordem na placa. Deixe suas respostas finais em notação de produto ou de fatorial.
Na ordem LLAAALL, tem-se:
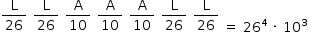
Assim, há um total de 264 · 103 placas possíveis nesse formato.
Pode-se obter agora o número de ordens em que pode ser formada a placa.
A placa possui 7 elementos, sendo 4 letras e 3 algarismos.
Dessa forma, há 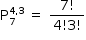 ordens diferentes.
ordens diferentes.
Se cada ordem possui 264 · 103 placas, o total de placas, independentemente da ordem, é