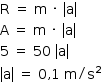Um rapaz de 50 kg está inicialmente parado sobre a extremidade esquerda da plataforma plana de um carrinho em repouso, em relação ao solo plano e horizontal. A extremidade direita da plataforma do carrinho está ligada a uma parede rígida, por meio de uma mola ideal, de massa desprezível e de constante elástica 25 N/m, inicialmente relaxada.
O rapaz começa a caminhar para a direita, no sentido da parede, e o carrinho move-se para a esquerda, distendendo a mola. Para manter a mola distendida de 20 cm e o carrinho em repouso, sem deslizar sobre o solo, o rapaz mantém-se em movimento uniformemente acelerado.

Considerando o referencial de energia na situação da mola relaxada, determine o valor da energia potencial elástica armazenada na mola distendida de 20 cm e o módulo da aceleração do rapaz nessa situação.
A energia potencial elástica armazenada na mola, nas condições do enunciado, é dada por:
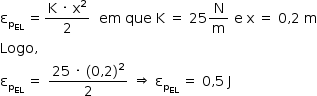
Na figura a seguir, estão representadas as forças ou componentes sobre o carrinho e o rapaz na direção horizontal, na situação em que a mola está distendida de 20 cm.
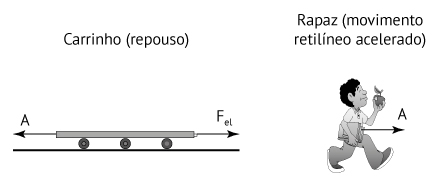
Como o carrinho encontra-se em em equilíbrio, a resultante é nula. Logo,
A = FEL ⇒ A = K · x ⇒ A = 25 · 0,2  A = 5 N
A = 5 N
Utilizando-se o Princípio Fundamental da Dinâmica no rapaz, obtém-se: