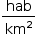A densidade populacional de cada distrito da cidade de South Hill, denotada por D (em número de habitantes por km2), está relacionada à distância x, em quilômetros, do distrito ao centro da cidade. A fórmula que relaciona D e x é dada por D = 5 + 30x – 15x2 .
a) Um distrito, localizado no centro da cidade de São Paulo, tem densidade populacional de 16,5 hab/km2 . Comparando a densidade populacional do distrito que fica no centro da cidade de South Hill com a do distrito do centro da cidade de São Paulo, a segunda supera a primeira em y%. Calcule y.
b) Determine a que distância do centro da cidade de South Hill a densidade populacional é máxima. Qual é o valor dessa densidade máxima?
a) A densidade populacional do distrito que fica no centro de South Hill é dada por D(0).
D(0) = 5 + 30 · 0 – 15 · 02 
D(0) = 5.
A diferença entre as densidades populacionais é dada por 16,5 – 5.
Tem-se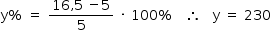 
Resposta: 230
b) Sendo a, b e c constantes reais, com a < 0, e y = c + bx + ax2, em que x e y são variáveis reais, y tem um valor máximo, e esse é obtido com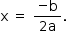 
Com D = 5 + 30x – 15x2, o valor máximo de D é obtido com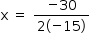 
, ou seja, com x = 1.
Com x = 1, tem-se D = 5 + 30 · 1 – 15 · 12, ou seja D = 20.
Resposta: 1 km e 20 