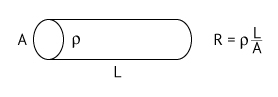
Um fio metálico homogêneo tem comprimento L e área de secção transversal constante. Quando submetido a uma diferença de potencial de 12 V, esse fio é percorrido por uma corrente elétrica de intensidade 0,1 A, conforme a figura 1. Esse fio é dividido em três partes, A, B e C, de comprimentos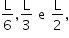 
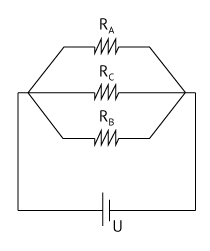
respectivamente, as quais, por meio de fios de resistências desprezíveis, são conectadas entre si e submetidas à mesma diferença de potencial constante de 12 V, conforme a figura 2.
Com base no circuito representado na figura 2, calcule:
a) a resistência equivalente, em Ω.
b) a potência total dissipada, em W.
a) Note-se que a associação sugerida na figura 2 corresponde a um paralelo de resistores. Assim, a resistência equivalente fica determinada:
