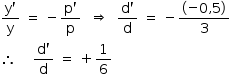Na entrada de uma loja de conveniência de um posto de combustível, há um espelho convexo utilizado para monitorar a região externa da loja, como representado na figura. A distância focal desse espelho tem módulo igual a 0,6 m e, na figura, pode-se ver a imagem de dois veículos que estão estacionados paralelamente e em frente à loja, aproximadamente a 3 m de distância do vértice do espelho.

Considerando que esse espelho obedece às condições de nitidez de Gauss, calcule:
a) a distância, em metros, da imagem dos veículos ao espelho.
b) a relação entre o comprimento do diâmetro da imagem do pneu de um dos carros, indicada por d na figura, e o comprimento real do diâmetro desse pneu.
a) A partir do enunciado:
- distância do objeto ao espelho: 3 m ⇒ p = 3 m
- espelho convexo de distância focal 0,6 m ⇒ f = –0,6 m
A partir da equação de Gauss:
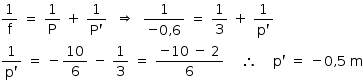
Logo, a distância da imagem dos veículos ao espelho é 0,5 m.
b) Considerando-se que:
- d é o diâmetro do pneu
- d' é o diâmetro da imagem do pneu
A partir da equação do aumento linear transversal: