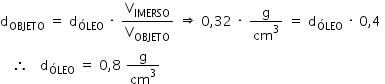Um objeto homogêneo colocado em um recipiente com água tem 32% de seu volume submerso; já em um recipiente com óleo, tem 40% de seu volume submerso. A densidade desse óleo, em g/cm3, é
Note e adote:
Densidade da água = 1 g/cm3
A figura a seguir representa as forças aplicadas em um corpo parcialmente imerso em um líquido.
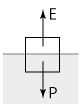
Considerando que nas situações descritas no enunciado o corpo se encontra em equilíbrio, para ambas as situações, pode-se dizer que:
E = P ⇒ dLÍQUIDO . VIMERSO .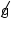 
= dOBJETO . VOBJETO .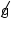
dOBJETO = dLÍQUIDO .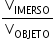 
- Quando o corpo está imerso na água:
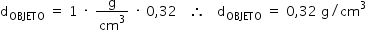
- Quando o corpo está imerso no óleo:
