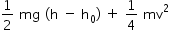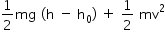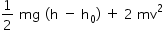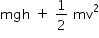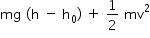Uma bola de massa m é solta do alto de um edifício. Quando está passando pela posição y = h, o módulo de sua velocidade é v. Sabendo-se que o solo, origem para a escala de energia potencial, tem coordenada y = h0, tal que h > h0 > 0, a energia mecânica da bola em y = (h - h0)/2 é igual a
Note e adote:
Desconsidere a resistência do ar.
g é a aceleração da gravidade.
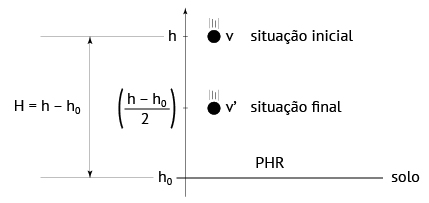
A partir do enunciado, a situação pode ser esquematizada como se segue:
A energia mecânica inicial é dada por:
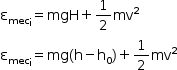 ,
,
pois em y = h0 é considerado o plano horizontal de referência (PHR).
Como o sistema é conservativo, a energia mecânica final é igual à energia mecânica inicial. Logo, a alternativa correta é E.