Uma dieta de emagrecimento atribui a cada alimento um certo número de pontos, que equivale ao valor calórico do alimento ao ser ingerido. Assim, por exemplo, as combinações abaixo somam, cada uma, 85 pontos:
• 4 colheres de arroz + 2 colheres de azeite + 1 fatia de queijo branco.
• 1 colher de arroz + 1 bife + 2 fatias de queijo branco.
• 4 colheres de arroz + 1 colher de azeite + 2 fatias de queijo branco.
• 4 colheres de arroz + 1 bife.
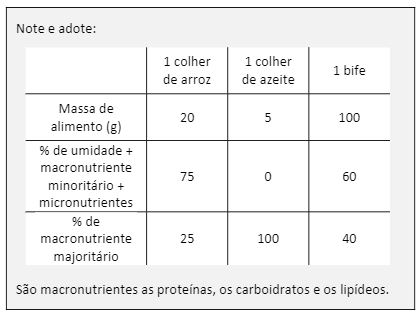
Com base nas informações fornecidas, e na composição nutricional dos alimentos, considere as seguintes afirmações:
I. A pontuação de um bife de 100 g é 45.
II. O macronutriente presente em maior quantidade no arroz são os carboidratos.
III. Para uma mesma massa de lipídeo de origem vegetal e de carboidrato, a razão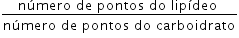 
é 1,5.
É correto o que se afirma em
Sendo:
- x a pontuação referente a uma colher de arroz;
- y a pontuação referente a um colher de azeite;
- z a pontuação referente a uma fatia de queijo branco;
- w a pontuação referente a um bife,
tem-se o sistema:
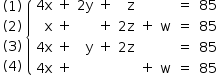
De (1) — (3) tem-se: y = z
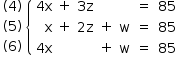
De (4) – (6), tem-se: w = 3z
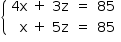
Resolvendo o sistema, obtêm-se: z = 15 e x = 10.
Assim, w = 45 e y = 15.
Analisando as alternativas, tem-se:
I. Correto. Pelo sistema, a pontuação de um bife de 100 g é 45.
II. Correto. O macronutriente presente em maior quantidade no arroz são os carboidratos, assim como no azeite é o lipídio de origem vegetal.
III. Correto. Pela análise da tabela, tem-se:
