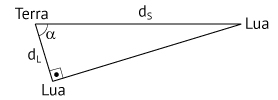
Quando a Lua está em quarto crescente ou quarto minguante, o triângulo formado pela Terra, pelo Sol e pela Lua é retângulo, com a Lua no vértice do ângulo reto. O astrônomo grego Aristarco, do século III a.C., usou este fato para obter um valor aproximado da razão entre as distâncias da Terra à Lua, dL, e da Terra ao Sol, dS.
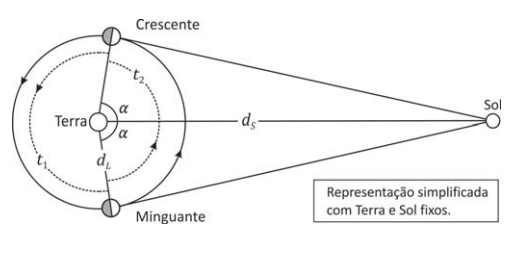
É possível estimar a medida do ângulo α, relativo ao vértice da Terra, nessas duas fases, a partir da observação de que o tempo t1, decorrido de uma lua quarto crescente a uma lua quarto minguante, é um pouco maior do que o tempo t2, decorrido de uma lua quarto minguante a uma lua quarto crescente. Supondo que a Lua descreva em torno da Terra um movimento circular uniforme, tomando t1 = 14,9 dias e t2= 14,8 dias, conclui-se que a razão dL/dS seria aproximadamente dada por

Em um M.C.U., os arcos percorridos são proporcionais aos intervalos de tempo. Logo:
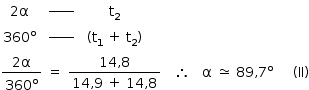
De (I) e (II), tem-se que:
