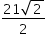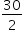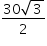Cada aresta do tetraedro regular ABCD mede 10. Por um ponto P na aresta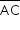 
, passa o plano α paralelo às arestas 
Dado que AP = 3, o quadrilátero determinado pelas interseções de α com as arestas do tetraedro tem área igual a
- a
21
- b
- c
30
- d
- e
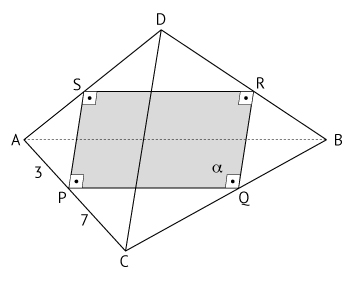
Sejam Q, R e S os pontos de intersecção de 
com as arestas 
, 
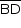e 
, respectivamente.
Como duas arestas reversas de um tetraedo regular são ortogonais,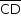 
é ortogonal a 
.
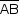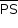é paralela a 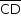e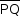 
é paralela a 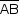. Logo, 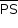é perpendicular a 
.
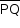Analogamente,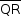 
é perpendicular a 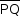e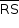 
é perpendicular a 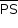. Portanto, o quadrilátero 
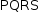é um retângulo.
Como AC = 10 e AP = 3, logo PC = 7.
Os triângulos APS e BQR são equiláteros de lado igual a 3.
Os triângulos CPQ e DRS são equiláteros de lado igual a 7. Portanto, a área do quadrilátero PQRS é: 3 · 7 = 21.