Os pontos A , B e C são colineares, AB = 5, BC = 2 e B está entre A e C. Os pontos C e D pertencem a uma circunferência com centro em A. Traça-se uma reta r perpendicular ao segmento passando pelo seu ponto médio. Chama-se de P a interseção de r com
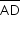 . Então, AP + BP vale
. Então, AP + BP vale
Uma construção possível, seguindo o enunciado, é:
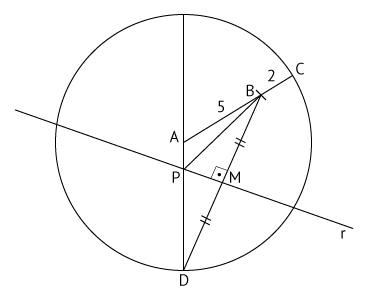
Como AB = 5 e BC = 2, então o raio da circunferência é 7.
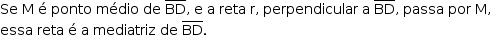 .
.
Logo, DP = BP
Assim,
AP + BP = AP + DP
= raio
= 7