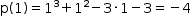Considere o polinômio cúbico p(x) = x3 + x2 - ax -3, onde a é um número real. Sabendo que r e −r são raízes reais de p(x), podemos afirmar que p(1) é igual a
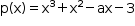
Raízes: x, r e -r
Soma das raízes = 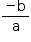 (Relações de Girard)
(Relações de Girard)
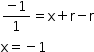
Se – 1 é raiz, então 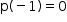
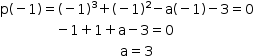
Portanto 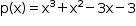
Logo, tem-se que