Considere o círculo de equação cartesiana x2 + y2 = ax + by , onde a e b são números reais não nulos. O número de pontos em que esse círculo intercepta os eixos coordenados é igual a
A figura dada pela equação x2 + y2 = ax + by intersecta o eixo das abscissas nos pontos em que y = 0 e o eixo das ordenadas nos pontos em que x = 0.
Assim:
• Intersecções com o eixo das abscissas:
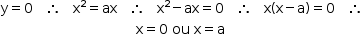
Logo, as intersecções são os pontos (0, 0) e (a, 0).
• Intersecções com o eixo das ordenadas:
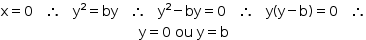
Logo, as intersecções são os pontos (0, 0) e (0, b).
Como a ≠ 0 e b ≠ 0, a figura intersecta os eixos coordenados em 3 pontos distintos.