Considere a matriz quadrada de ordem 3, 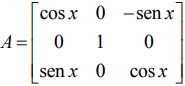 , onde x é um número real.
, onde x é um número real.
Podemos afirmar que
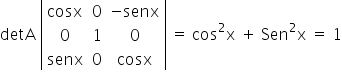
Como detA ≠ 0, A é invertível para todos os valores de x.
Considere a matriz quadrada de ordem 3, 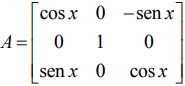 , onde x é um número real.
, onde x é um número real.
Podemos afirmar que
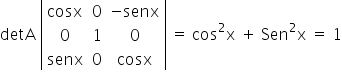
Como detA ≠ 0, A é invertível para todos os valores de x.