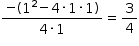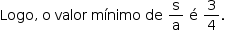Seja (a, b, c) uma progressão geométrica de números reais com a ≠ 0 . Definindo s = a + b + c, o menor valor possível para s/ a é igual a
Considere a P.G.: (a, aq, aq2), a ≠ 0
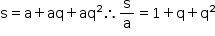
O valor mínimo de q2 + q + 1 é
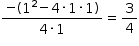
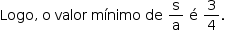
Seja (a, b, c) uma progressão geométrica de números reais com a ≠ 0 . Definindo s = a + b + c, o menor valor possível para s/ a é igual a
Considere a P.G.: (a, aq, aq2), a ≠ 0
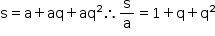
O valor mínimo de q2 + q + 1 é